SHM: Basic Concepts

Undulatory
/
Simple Harmonic Motion
/
SHM: Basic Concepts

In nature we often find phenomena that recur continuously: the seasons of the year, the phases of the moon and our heart beats are examples of these phenomena. The simple harmonic motion (SHM) is a model that describes several phenomena of this type, so any simple harmonic motion is periodic and oscillatory.

Basic Concepts

We present two definitions for SHM:

Def. 1: It is the motion performed by an object around a fixed point. The force intensity that generates this motion is proportional to the displacement from the fixed point and the direction is to move the object in the direction of the fixed point position. The force in the SHM is of the type: $ F \propto x $, where $x$ is the displacement relative to the equilibrium position. Note: The symbol "$\propto$" denotes proportionality.
Def. 2: It is called SHM any movement that obeys a law represented by a sinusoidal (or cosine) function of the type: $$ x = A sin(\omega t + \theta_0)$$ or $$ x = A cos(\omega t + \theta_0)$$

Other important definitions are:

Periodic Motion: It is every movement where the same situation is repeated in equal time intervals.
Oscillatory Motion (Vibration): It is all symmetrical movement around a fixed point.

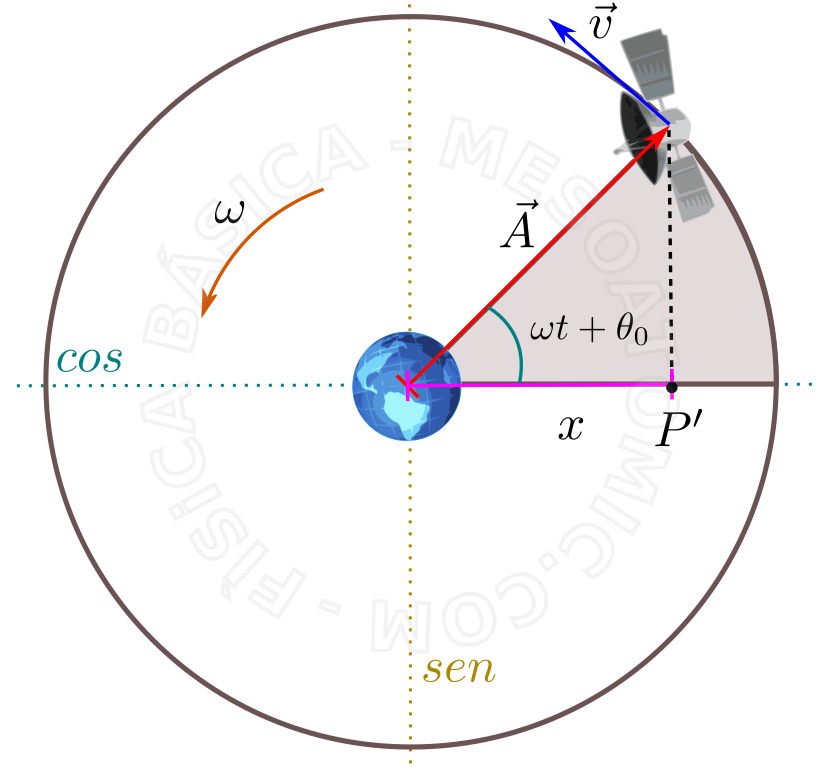
**Illustration of SHM.** The satellite that moves in a uniform circular motion (UCM) can be seen as an SHM if we consider only the component $x$ (or $y$ ) of the position vector $\vec{A}$. The vector $\vec{A}$ rotates anti-clockwise around a fixed point (in this case Earth) with angular velocity $\omega$ and makes an angle $ \omega t + \theta_0 $ with the x-axis.

Time Functions of SHM:

To write the position as fuction of time for the SHM we need to know:

Amplitude ( $A$ ): It is the measure of maximum displacement of the system from the fixed point.
Initial Phase ( $\theta_0$ ):: It is the deviation from the fixed point at the initial time, $t = 0$.
Angular Velocity ( $\omega$ ):: It is the the amount of repeated events in a time interval, or angular frequency of the movement. It is given by $$ \omega = \frac{2 \pi}{\tau} = 2 \pi f,$$ where $\tau$ is the period and $f$ the motion frequency.

With this, we have:

Elongation ( $x$ ): It is the distance from the system to the fixed point, and is given by: $$x = A cos ( \omega t + \theta_0 ).$$
Speed ( $v$ ): $v = -\omega A sin ( \omega t + \theta_0 )$
Acceleration ( $a$ ): $a = -\omega^2 A cos ( \omega t + \theta_0 )$

Speed in Function of Elongation:: $v = \omega^2 (A^2- x^2) $
Speed at The Turning Point:: $v = 0 $
Speed at The Central Point:: $v = \pm \omega^2 x $ (Max and Min)
Acceleration Due to Elongation:: $a = -\omega^2 x $
Acceleration in The Turning Point:: $a = \pm \omega^2 A $ (max and min).
Acceleration at The Midpoint:: $a = 0 $

In our APP you shall find: Offline Content Progress controller Hundreds of examples with solutions Calculator and Unit Converter And much more!!!

Basic Concepts

Time Functions of SHM:

STUDY PHYSICS ANYTIME ANYWHERE