- Optics
- /
- Reflection and Mirrors
- /
- Flat mirrors
"The mirror tests the reflection of light and the thoughtlessness of men".
Gar-Mar
The Plane Mirror
It is a stigmatic optical system, since it always relates an object point with a point image. It also relates a real object with a virtual image, upright and of the same size of the object. There is an inversion of the image relative to the axis parallel to the mirror, but there is no reversal from top to bottom (see figure below). We call this type of image specular or regular.

- Visual Field
- It is the region of space which can be observed through the mirror.
-

Illustration of the visual field (gray area) of an observer in a plane mirror. - Mirror Translation
- When a flat mirror is moved parallel to its initial position, the image of a fixed object undergoes an offset that is twice the mirror's displacement in the same direction.
-
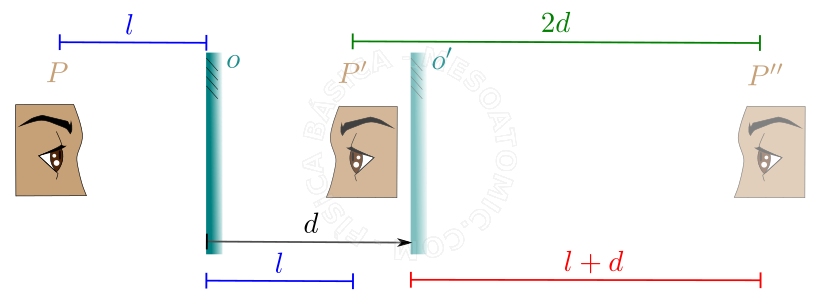
Displacement of a plane mirror. For an object at point \(P\) and a mirror at position \(o\), an image at point \(P'\) is generated. If the mirror is translated from position \(o\) to \(o'\), the image will move from point \(P'\) to the point \(P''\). As the mirror was moved at a distance \(d\), the image is transferred from a distance \(2d\). - Mirror Rotation
- If a plane mirror suffers a rotation of an angle \(\alpha\) around a vertex of the mirror, the reflected beam undergoes a rotation \(2\alpha\). This result is deduced using the laws of reflection and geometry (see figure below).
-
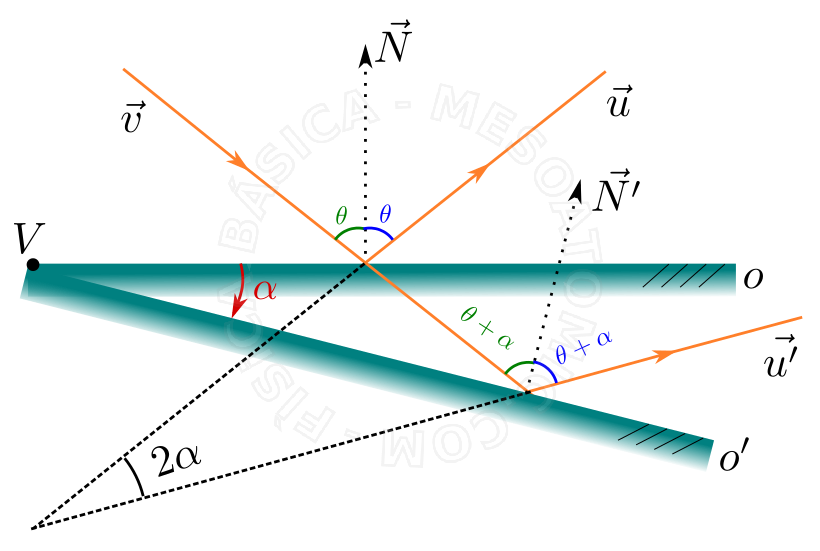
Rotation of a plane mirror. Consider an incident beam \(\vec{v}\) in a plane mirror \(o\), which has reflected beam \(\vec{u}\). If we rotate the mirror at an angle \(\alpha\), in relation to the vertex \(V\), to position \(o'\), the transmitted beam \(\vec{u}\) is rotated to \(2 \alpha\), assuming the direction \(\vec{u'}\). - Plane Mirrors Association
- If we associate two plane mirrors, so that they have an angle \(\alpha\) between them, we will have \(n\) images for an object \(P\) located between the mirrors, such that: \begin{equation} n=\frac{360}{\alpha}-1, \end{equation} where \( 0^o \lt \alpha \lt 180^o\) . The expression is only valid for values \(\alpha\) which are divisible by \(360\), for example, \(120^{o}\), \(90^{o}\), \(72^{o}\), etc. When \(\frac{360}{\alpha}\) is an odd integer, the expression is only valid for an object located at the bisecting line of the angle \(\alpha\).
-

Association of two mirrors with a right angle between them ( \(\alpha = 90^o\) ). In this case we have \(n = \frac{360}{90} - 1 = 3\) images.
