- Mechanics
- /
- Static
- /
- Static of solids
There are two simple ways of movement in a rigid system: translation and rotation. Any other possible form of movement, as complex it may be, can always be considered as the combination of a rotation and a translation.
Static Solid
It is not always possible to consider a body as a point particle, in general, when we are interested not only in the displacement of an object, but also in its rotation. The following definition is important:
- Rigid Body
- The model adopted for large objects considers that the size and shape of these are practically unaltered when subjected to external forces, although the actual molecular bonds are not perfectly rigid. Bridges, airplanes and many other objects can be considered good examples of rigid bodies. When they receive the action of very strong forces, they are little deformed, or on a extreme case, they get broken.
The two possible types of motion of a rigid body can be defined as:
- Translation
- It is the movement which changes the position of an object, i.e., all points of the body are moved from a fixed distance in the same direction.
- Rotation
- In rotational motion all points of the body move in circumferential arcs, whose centers are on the same axis, called the axis of rotation.
Balance of solids
For a solid to be in equilibrium in an inertial frame, it is necessary to satisfy two conditions: one relating to the balance of translation and other related to the rotation balance, defined as follows:
- Translational Balance
- The condition of translational equilibrium of a rigid body is that the center of mass is at rest or in uniform rectilinear motion, or the resultant of external forces acting on the body is zero. In mathematical form it is: $$\vec{F}_{net} = \vec{0}$$ where \(\vec{F}_{net}\) is the resultant of the forces in the system.
- Rotational Balance
- The condition of rotational equilibrium is that the body does not rotate or rotates in a uniform circular motion. For this to happen, in a rigid body under the action of a system of forces, it is necessary that the sum of moments of all forces about any axis be zero. In mathematical form it is: $$ \vec{M_{net}} = \vec{0},$$ where \(\vec{M_{net}}\) is the resultant torque on the system.
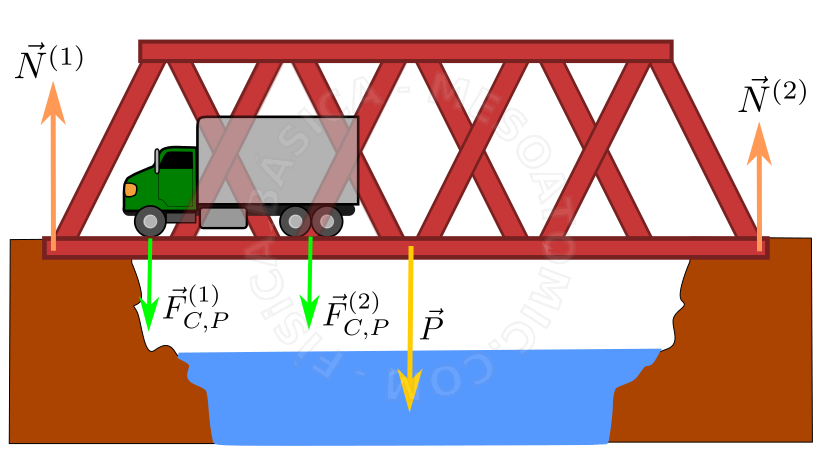
The figure above illustrates an extensive body, the bridge, suffering the action of various forces. Whereas the system of interest is the bridge, since we desire it to stay in a static equilibrium, the forces acting in it must meet the following conditions: to have no translation, the resultant should be zero, \begin{align} +& \vec{N}^{(1)} + \vec{N}^{(2)} + \vec{F}_{T,B}^{(1)} +\\ +& \vec{F}_{T,B}^{(2)} + \vec{P} = 0, \end{align} and so, to not have a rotation, the torque on the bridge must also be zero \begin{align} -& N^{(1)} d_{1} + N^{(2)} d_{2} + F_{T,B}^{(1)} d_{3} +\\ +& F_{T,B}^{(2)} d_{4}+ P d_{5}= 0, \end{align} where each \(d_i\) is the distance of each force in respect to the bridge's center of mass (position of vector \(P\)), then \(d_5 = 0\).
Lamy's Theorem
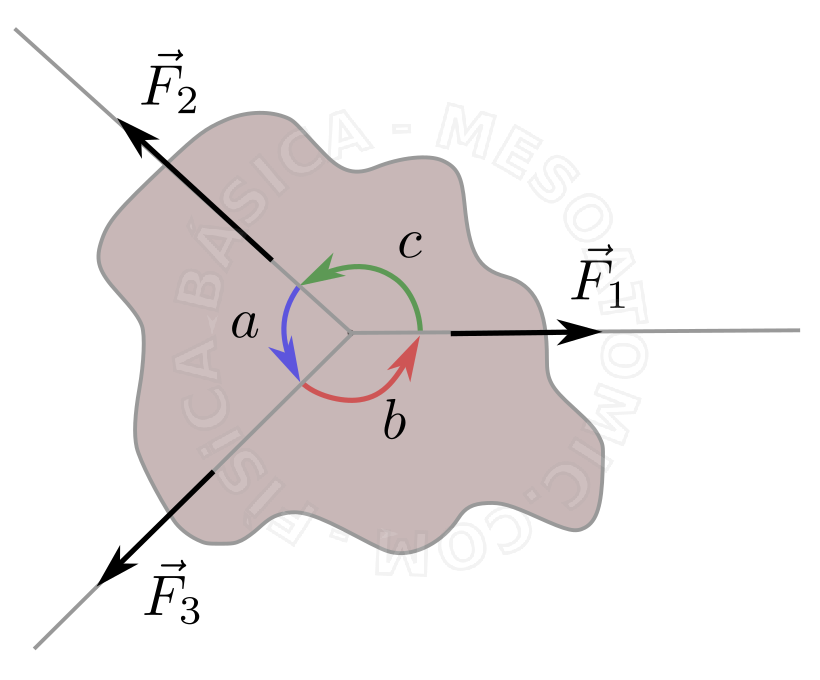
If a rigid system is in equilibrium under the action of only three external forces, \(F_1\), \(F_2\) and \(F_3\), not parallel, the module of each is proportional to the sine of the angle between the other two, namely: $$ \frac{F_1}{sen(a)} = \frac{F_2}{sen(b)} = \frac{F_3}{sen(c)},$$ where \(a\), \(b\) and \(c\) are the angles between the forces, as shown in the figure below.
Poisont's Theorem
Any system of forces, as complex as it seems, can always be reduced to a single force, known as the net force, and a torque. The torque and net force are orthogonal, always.
