The determination of the center of mass is performed through weighted average: \begin{array} \\ X_{cm} &=\frac{m_1 x_1+m_2 x_2 +...+ m_n x_n}{m_1+m_2+...+m_n},\\ Y_{cm} &=\frac{m_1 y_1+m_2 y_2 +...+ m_n y_n}{m_1+m_2+...+m_n}, \end{array} where the main factor \(m_i\) is the mass \(i\) -th particle and \((x_i,y_i)\) is its position as shown in the figure below.

• The center of mass of an isolated system, i.e., where the resultant of the forces is zero, it moves in uniform rectilinear motion, MRU, in any inertial frame.
• The center of mass of a particle system moves as if it were a single particle system subject to the same forces as a whole. In this case, it is considered that the total mass of the system is concentrated on this single particle.
• The total momentum of a system is equal to the product of the total mass center of mass velocity.
• The center of mass of a system that has uniform mass distribution is the actual geometric center (centroid).

Continuous Delivery

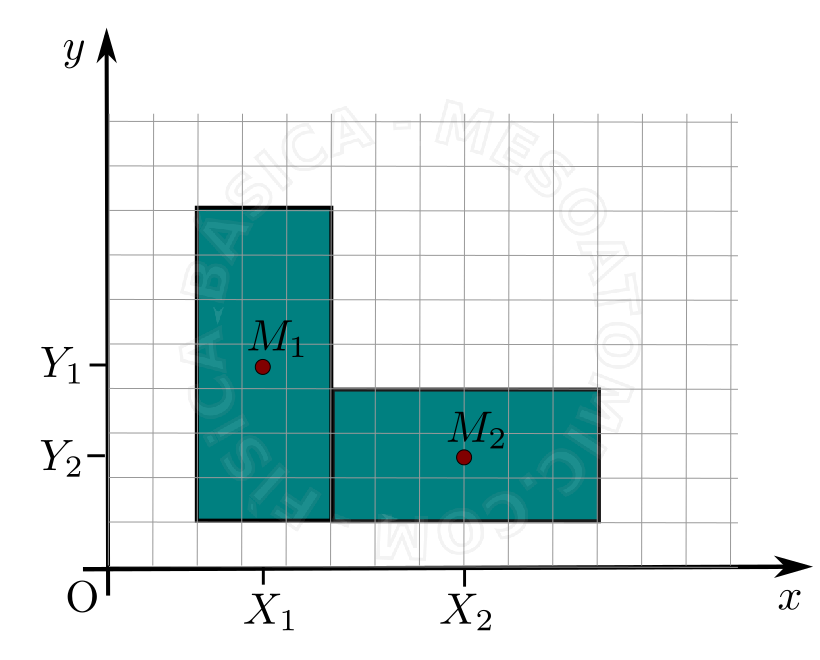
For the case of a continuous body as shown in the figure above, it is possible to simplify the calculation considering that the body is composed of two rectangles where the distribution of the mass is homogeneous. In this case, the center of mass of each rectangle is in its respective centroid and the system mass center as a whole. The two rectangles can be calculated with the formulas: \begin{align} X_{CM} &= \frac{X_1 M_1 + X_2 M_2}{M_1 + M_2},\\ Y_{CM} &= \frac{Y_1 M_1 + Y_2 M_2}{M_1 + M_2}, \end{align} where \((X_1, Y_i)\) is the mass center position of the total mass of object \(M_i\).