- Mechanics
- /
- Dynamics
- /
- Work and power
Work is a process by which energy can be transformed from one form to another or transferred from one object to another, due to the action of a force.
Work of a force
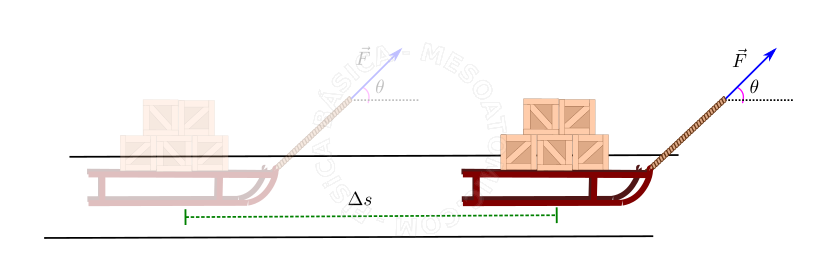
The work unit is Joule, \([w] = J\) .
It is important to note that the work is not a vector quantity, but a scalar.
You can find the following formulas for the work of the different mechanical forces:
- Work done by weight \((w_g)\)
- The work to move \(\Delta h\) a mass body \(m\) in the gravitational field of acceleration \(g\) is: $$ w_g(h) = mg \Delta h.$$ Note that this work only depends on the vertical displacement (height).
The weight force does not perform work on the horizontal! - Work done by springs \((w_e)\)
- The work required to stretch a spring of elastic constant \(k\) from its rest position \(x`\) to a position \(x\) is: $$ w_e(\Delta x) = k \frac{(\Delta x)^2}{2},$$ where \(\Delta x = (x`-x)\).
- Work done by a generic force \((w)\)
- It is the area under the curve of a graph. One must plot the tangetial force to the trajectory \(versus\) the displacement.
Work and Time
For machines, it is interesting to measure the amount of work that they are able to produce per unit of time; this quantity is known as power. So, it is possible to know how long it takes for a machine to produce the desired effect.
Another important variable is the efficiency, because for a machine to do some work, first, it is necessary to supply power to the machine, or capacity to do work. There is always some loss in this process. The cost versus benefit of this process is given by the efficiency.
The quantities above can be defined as follows:
- Power \((P)\)
- It is the work done per unit time, $$ P = \frac{w}{\Delta t},$$ and its unit in the \(IS\) is Watt, \([P]=W\).
- Efficiency \((\eta)\)
- It is the ratio of the net power \(P_n\) and the total power \(P_t\), $$ \eta = \frac{P_{n}}{P_{t}}.$$ This quantity is dimensionless. The useful power can never be greater than the total power supplied to the system, so, \(\eta\) is in the range \([0,1]\). A good efficiency is close to 1 and a poor efficiency is close to 0.
