- Physics
- /
- Mechanics
Select the subtopic
Basic motions
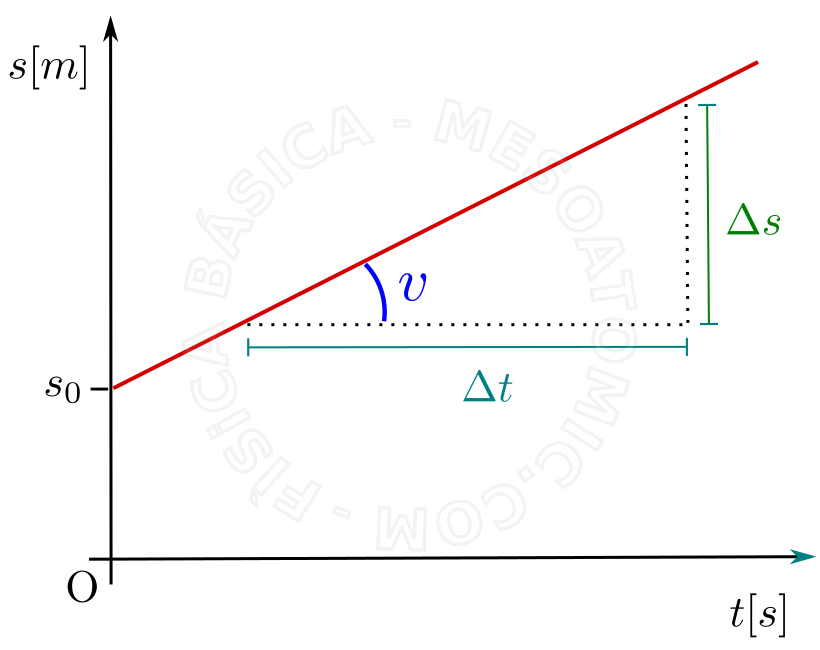
Consider a car that is pouring oil, so that oil drips at equal intervals of time. The positions of the oil marks on the track can be used to understand the movement of this car. In the...
Vertical launch

Vertical launch is the rectilinear and vertical motion that an object describes when it is only under the gravitational force action and where the air resistance is neglected.
Vector kinematics
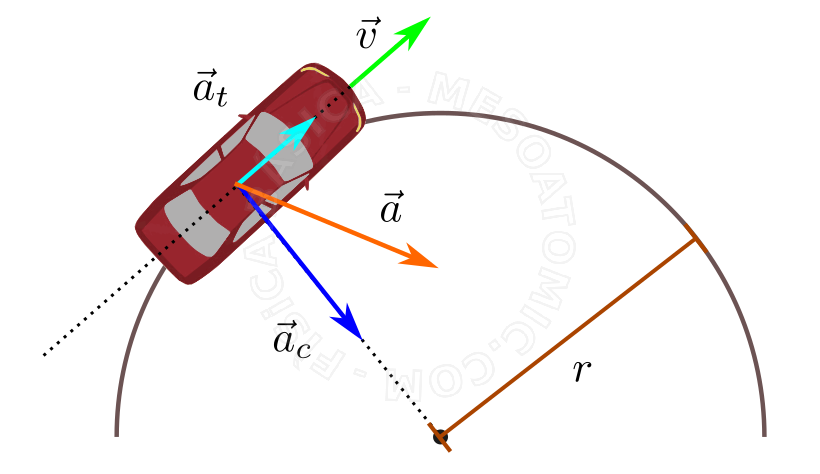
When a movement occurs in two dimensions or more, one will need to work with vectors, i.e., one must use the vector kinematics. One example of movement in two dimensions is a car describing a...
Circular motion

Circular motion is the movement whose trajectory describes a circular arc.
Relative motion
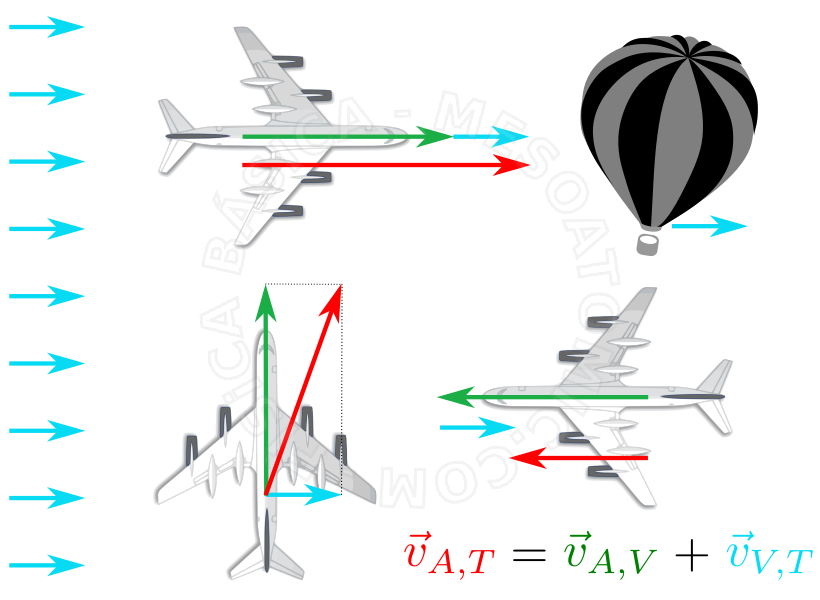
When we observe a phenomenon in nature, we can do this from different places and ways. For example, when watching the movement of a car, we can observe it by standing on a sidewalk or we can...
Oblique throw
The launch of any object whose initial velocity forms an angle (other than \(90^o\) ) with the Earth's surface is called oblique throw. Here, we consider only the case without friction; that is,...

