Principles of hydrostatics

Fluids
/
Hydrostatic
/
Principles of hydrostatics

To describe the behavior of fluids in different situations, it is important to know the basic principles.

Basic Principle of Hydrostatic (Stevin's Principle)

The difference between the pressures of two different points within a liquid in equilibrium is proportional to the density of the liquid, $\rho$, the gravity acceleration module, $g$, and the differences in the heights of the points considered $h$. Mathematically, we have $$\Delta P = P_B - P_A = \rho g h.$$

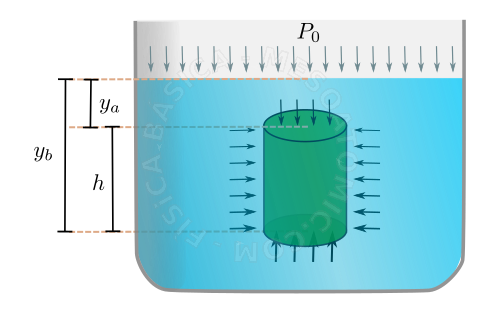
**Pressure on a submerged object.** When an object is submerged in a fluid, in addition to atmospheric pressure $P_0$, the liquid also puts pressure on the walls of this object, which increases with depth. In the figure, a green cylinder is submerged in a liquid. Note that the forces on the sides of the cylinder cancel each other out, but the pressure at the top ($P_t = P_0 + \rho g y_a$) is less than the pressure at the bottom ($P_b = P_0 + \rho g y_b$). With this, there is a resulting hydrostatic force pushing out the cylinder. Depending on the weight, the cylinder may float or sink.

The distribution of pressure in a fluid is due to:

the existence of a gravitational field
an acceleration of the fluid by external forces (non-gravitational)
a combination of both causes.

Importantly, for the air, as the density is very low, we can ignore the pressure variation with height when this variation is of the order of a few meters.

Consequences of Stevin's Principle

Points that support the same pressure belong to a same horizontal plane. Effect: The whole free surface of a liquid in equilibrium is horizontal.

Principle of communicating vessels. No matter the geometry of the containers, if the liquid can freely pass from one to the other, the horizontal lines in these containers will have all the same pressures, which increase with depth ($P_h > P_0$) as established by Stevin's principle.
When immiscible liquids (those which do not mix) are placed in a container, they are disposed from the bottom to the top of the container, in descending order of their densities. The separation surface between two non-miscible liquids is flat and horizontal.

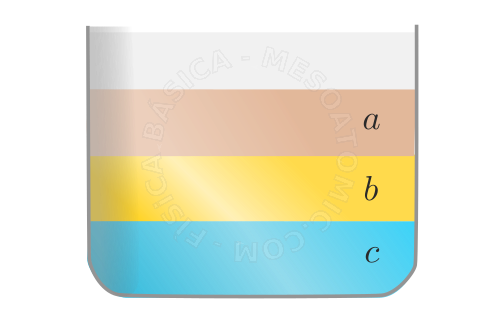
Immiscible liquids. The figure illustrates three liquids that do not mix, for example, liquid $a$ could be water, $b$ cooking oil and $c$ alcohol.
If two immiscible liquids are placed in a U-shaped tube, the heights reached by the liquids, from the separation surface, are inversely proportional to the specific masses of the liquids, i.e., $$ \frac{h1}{h2} = \frac{\rho_2}{\rho_1}.$$

Liquids immiscible in a U-shaped tube. In this case, the orange liquid has density $\rho_l$ which is less than the density of the blue liquid, $\rho_a$ , so it is on top. Although the surfaces are in contact with the air (free surfaces), but at different heights, due to the low density of the air, it is a good approximation to consider that the atmospheric pressure $P_0$ is the same on these two surfaces. With this we can relate the liquid densities to the heights, since $P_0 + \rho_l g h_1 = P_0 + \rho_a g h_2$ , i.e., $$\rho_l h_1 = \rho_a h_2.$$

Pascal's Law

A pressure variation occurring at any point in an equilibrium liquid is transmitted integrally to all points of the liquid.

That is, for a smaller area $a$ in relation to a bigger area $A$ in a fluid, a lower intensity force $f$ can balance a stronger force $F$, depending on the ratio $\frac{a}{A}$.

This principle is used in workshops, in the machines that suspend the cars and also in the brakes and directions of some vehicles.

In our APP you shall find: Offline Content Progress controller Hundreds of examples with solutions Calculator and Unit Converter And much more!!!

Basic Principle of Hydrostatic (Stevin's Principle)

Consequences of Stevin's Principle

Pascal's Law

STUDY PHYSICS ANYTIME ANYWHERE