- Fluids
- /
- Hydrostatic
- /
- Buoyancy
It is essential to understand the forces that an object undergoes when immersed in a fluid. The buoyancy force is one of them. This knowledge enables various applicationsb such as the development of ships, ferries, submarines and other aquatic devices. The easiest way to understand this force is through the principle of Archimedes.
Archimedes' Principle
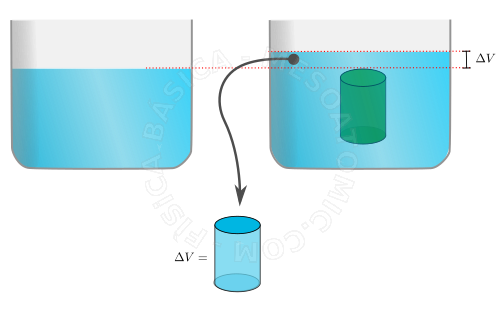
Any body immersed or floating in a fluid, within a gravitational field, is subject to the action of a force exerted by the fluid called buoyancy (\(E\)), which has the following characteristics:
- The value of the buoyancy module is equal to the weight of the displaced liquid volume.
- The direction axis of buoyancy is vertical from bottom up.
- The net force of buoyancy acts on the center of gravity of the displaced fluid, which is called impulse center.
Importantly, if only part of the body is immersed in the liquid, \(V_{body}\) should only correspond to the volume of the body part immersed in the liquid.
The figure below illustrates the principle of Archimedes.