To determine the magnetic field generated by a current it is needed to study the Biot-Savart law determining the magnetic field \(B\) at a point \(P\) due to a current element \(\Delta l\). With \(r\) being the vector module that goes from the current element to the point \(P\), the magnetic field is given by:

Module (or intensity)

$$\Delta B = \frac{\mu}{4 \pi}\frac{ i (\Delta l) sen(\theta)}{r^2}$$ where \(\theta\) is the angle formed by the vector \(\vec{r}\) and the direction of the current element \(\vec{i}\) and \(\mu\) is the magnetic permeability of the medium where the magnetic fild is in. In the case of vacuum we exchange \(\mu\) with \(\mu_0\).

Direction (or axis)

It is perpendicular to the plane formed by \(\vec{r}\) and \(\vec{\Delta l}\). Imagine a nail stuck on a wooden plank, the last one represents the plane.

The Biot-Savart is analogous to Coulomb's law used to calculate the electric field produced by a point charge. The source of the magnetic field is a charge \(q\) with velocity \(v\) or a current element \(i\) of length \(\Delta l\), in the same way a static load \(q\) is the source of an electric field. The magnetic field diminishes with the square of the distance from the current element in the same way as the electric field decreases with the square of the load's distance.

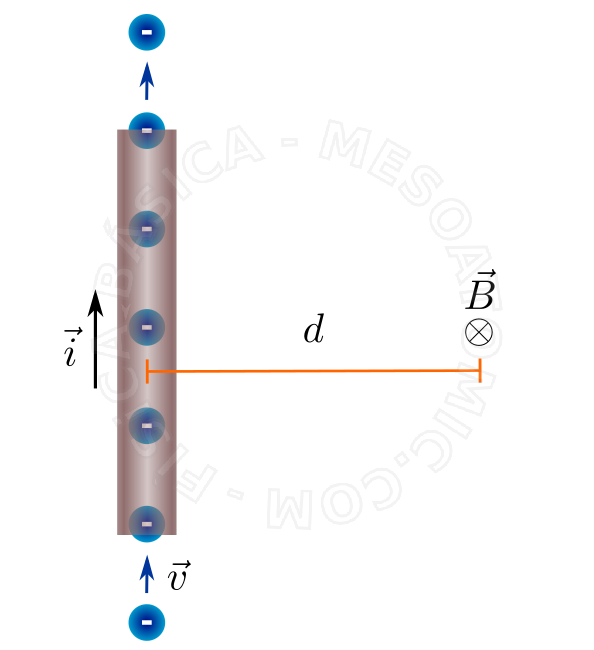
Rectilinear Infinite Wire

We can consider that a electric current is infinite if we are interested in an area that is much smaller than the length of the conductor, for example, a few centimeters from the middle of a wire several meters long. The field at a distance \(d\) of a long wire with electric current \(i\) is: $$B = \frac{\mu_0}{2 \pi} \frac{i}{d}$$ as it is illustrated in the figure below.

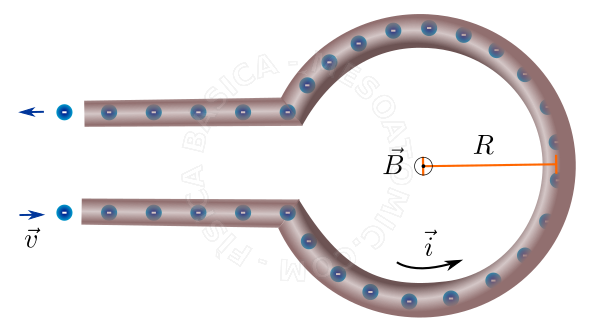
Circular Conductor

A circular loop has at its center a magnetic field which depends on the radius \(R\) of the current loop and the electric current \(i\), and its modulus is $$B = \frac{\mu_0 i}{2 R}.$$ The direction of \(\vec{B}\) is illustrated in the figure below.

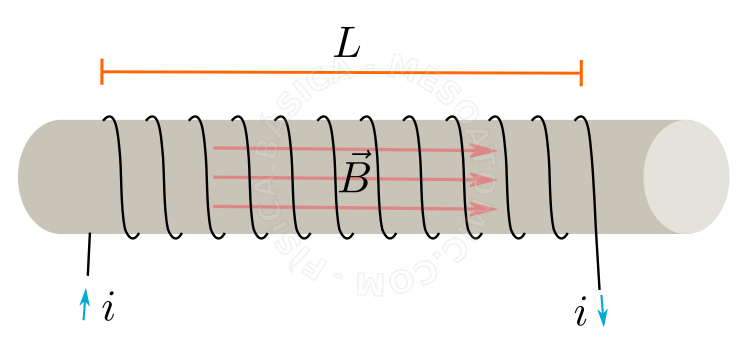
Solenoid Conductor (coil)

For an infinite solenoid, in other words, a much larger length than the region of interest, we have the magnetic field within this solenoid depending on the number \(N\) of turns comprising the solenoid and the length \(L\), that is the density of the number of turns. The field is given by: $$B = \frac{N}{L} \mu_0 i = n \mu_0 i.$$ The direction of the field is represented in the figure below.