The electric potential is related to the concept of potential energy \((U)\) acquired by a unit charge moving in an electric field. (Analogous to the gravitational potential energy, which refers to the displacement of a mass in a gravitational field.) By definition, any potential is a scalar quantity.

The electric potential \(\mathcal{V}_A\) at a point \(A\) is equal to the work \(w_{A \rightharpoonup O}\) made by an electrical force to carry a unity charge from a point \(O\) to the point \(A\). The position of the point \(O\) can be chosen arbitrarily. In general, we choose the position that facilitates the calculus.

For a finite set of charges, it is common to use the potential of the source, \(O\) , far away from these charges (at infinity), \( O \rightarrow \infty\) . Mathematically $$\mathcal{V}_A = \frac{w_{A \rightharpoonup \infty}}{q},$$ i.e., the work required to bring a charge \(q\) from infinity to the point \(A\), is closer to the charges that are generating the field.

The electric potential in the \(IS\) unit is Volt \([\mathcal{V}] = V = \frac{J}{C}\) (Joule per Coulomb).

The choice to represent electric potential using the letter \(V\) makes a lot of mess. Since \(V\) represents the electric potential, a unit, and also the potential difference. Since many other authors use this notation, it is the standard and we are better off using it also, but we will change the font.

Work of The Electric Force \((w_{A \rightharpoonup B})\) :

The work resulting from an electrical charge \(q\) in an electric field, that undergoes a displacement from point \(A\) to \(B\) , is given by: $$ w_{A \rightharpoonup B} = q (\mathcal{V}_B – \mathcal{V}_A ),$$ Where \(\mathcal{V}_A\) and \(\mathcal{V}_B\) are the potential values at the points \(A\) and \(B\) , respectively.

Electric Potential Energy \((U)\) :

It is the energy of a charge \(q\) at a point \(A\) in the presence of an external electric field. That is, the energy of the system is formed by the charges and the external field in which it is immersed. Mathematically: $$ U(A) = q \mathcal{V}_A$$ Where \(\mathcal{V}_A\) is the potential at the point \(A\) . The unit \(U\) is the Joule \((J)\) .

Potential Difference (\(\mathbb{V}\)):

The potential difference \(\mathbb{V}\) is equal to the work per unit charge, that an external agent must carry out to move a charge \(q\) in an electric field from a point \(A\) to point \(B\) without changing the kinetic energy of the charge. That is, the potential difference \(\mathbb{V}\) between points \(A\) and \(B\) is $$\mathbb{V}_{AB} \equiv \mathcal{V}_B – \mathcal{V}_A = \frac{w_{A \rightharpoonup B}}{q} = \frac{U(B) - U(A)}{q}.$$ Therefore, \(\mathbb{V}\) is also the difference in electric potential energy (Joules) per unit electric charge (Coulomb) .

Potential Due to a Punctual Charge:

The electric potential of a point charge \(q\) at a point \(A\) in relation to a reference point infinitely far is given by: $$ \mathcal{V}_A = k \frac{q}{d_A},$$ Where \(d_A\) is the shortest distance from the charge to point \(A\) . A positively charged particle has a positive electric potential and a negative one has a negative potential.

Electric Potential Due to a Set of Punctual Charges:

The potential due to a set of point charges at a certain point in space is equal to the sum of the potential of each charge.

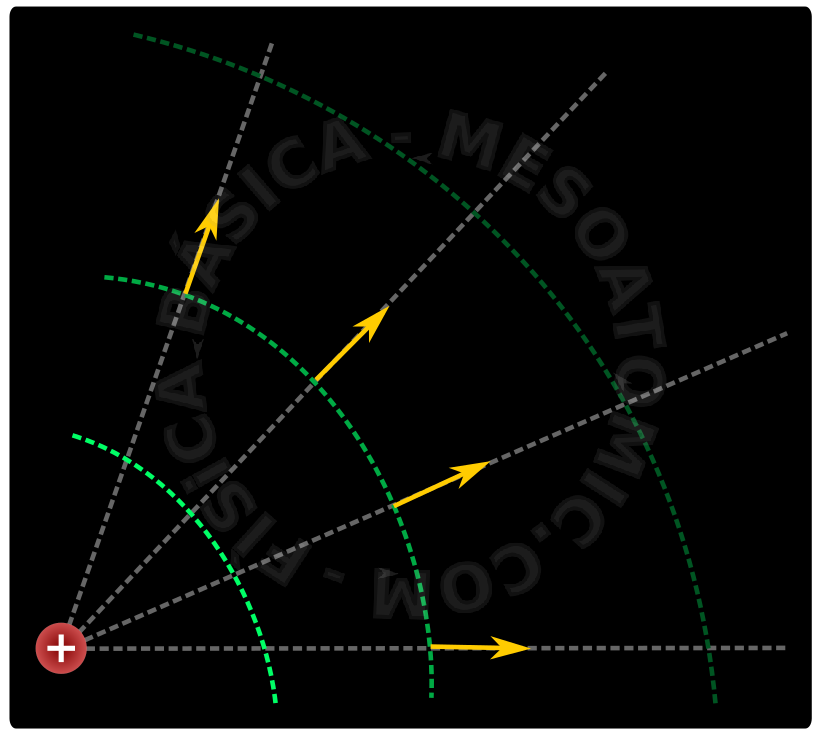
Field Lines:

The electric field lines point in the direction of decreasing potential.

Electronvolt:

It is a unit of energy commonly used in atomic and nuclear physics. It is defined as the energy that an electron or proton takes when moving through a potential difference of 1 volt, thus \(1eV=1.6 \times 10^{-19} J\) .

Equipotential Surfaces

Equipotential surfaces are regions of space where the potential always has the same value and the following characteristics:

• Points on an equipotential surface all have the same value;
• The work needed to move a test charge from one equipotential surface to another is independent of path the charge took to go from one surface to another. That is, the work only depends on the initial equipotential surface and the final surface.
• The electric field is perpendicular to the equipotential surfaces.