- Electromagnetism
- /
- Electrostatic
- /
- Electric field
It is a region of space where a test charge is subject to the action of a force of electrical origin.
Electric Field
It is said that an electric charge generates an electric field. The field intensifies as we approach this charge and will weaken as we move away from it. Therefore, the electric field \(\vec{E}\) is a function of the distance \(d\) between the charge and a point in space. $$\vec{E}=\vec{E}(d)$$ To calculate the electric force due to the electric field of a charge, we can use a test charge \(q_0\). Suppose \(d_0\) is the distance from the charge to the test charge, the force on the test charge, due to the field-generating charge, is: $$\vec{F} = q_0 \vec{E}(d_0).$$ The electric field unit in the \(IS\) is Newton per Coulomb \([E]=\frac{N}{C}\) .
- Electric Field of a Point Charge
- For a charge amount \(Q\) concentrated at one point, the electric field module in vacuum at a distance \(d\) from the charge, is $$E(d) = k_0 \frac{Q}{d^2}.$$
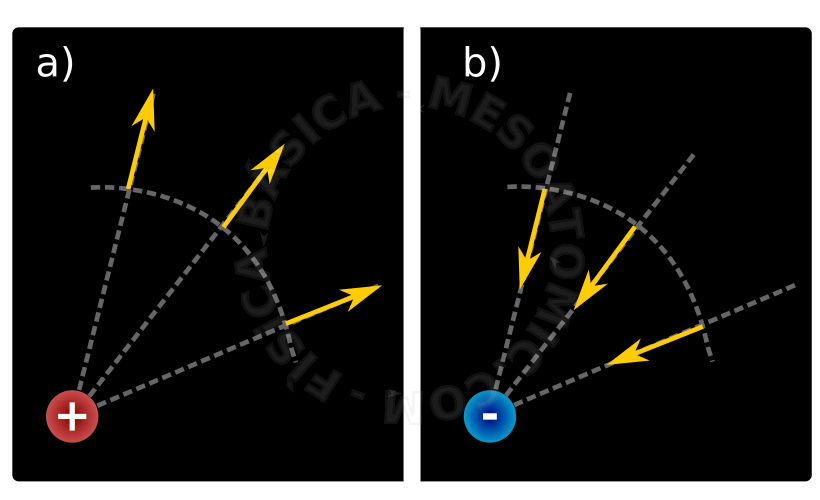
Illustration of the electric field, which is a vector quantity. For an equal distance from a punctual charge, the field has the same module (intensity), but different directions for different charges. The direction of the field at a given point is always parallel to the line that connects the charge to the point. For positive charges, the field points out; for negative charges, the field points to the charge. - Electric Field Due to a Set of Punctual charges
- To find the resulting electric field due to a set of punctual charges, it is necessary to add up vectorially the electric fields produced by each of the charges.
- Uniform Electric Field
- It is when the electric field vector has the same module and direction everywhere.
- Conductive Solid Sphere
- The electric field generated by a spherical surface uniformly charged has the following properties:
- The field is null inside.
- Considering the surrounding space of the sphere, the generated field is equivalent to a field generated by a punctual charge with the same amount of charges located in the center of the sphere.
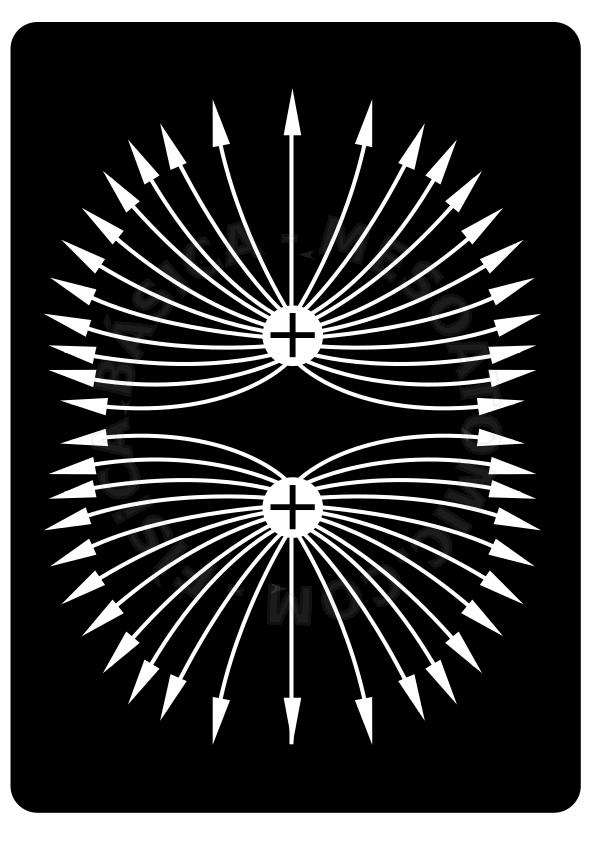
Field Lines
To facilitate the understanding of the electric field, we imagine "field lines".
The script for the construction of these lines is:
- The electric field vector is tangent, at each point, to the line of force at that point.
- The intensity of the electric field is proportional to the number of lines represented in the field;
- The lines start with positive charges, go to the negative charges and end there.
- The number of lines leaving a positive charge, or approaching a negative charge, is proportional to the number of electric charges at that point;
- Two lines never cross.