- Termofísica
- /
- Termodinâmica
- /
- Prim. Lei da Termodinâmica
No início do desenvolvimento da termodinâmica, ela era aplicada nos problemas que envolviam a transformação de calor em trabalho. Na atualidade, os métodos termodinâmicos se aplicam em múltiplas transformações físicas e químicas, para o estudo das propriedades das substâncias e de radiações.
Termodinâmica
- Sistema, vizinhança e fronteira.
- Uma região do espaço que se quer estudar denomina-se "sistema" e está separado do resto do universo ("meio externo" ou "vizinhança") através de uma superfície real ou imaginária denominada "fronteira".
-

Sistema Termodinâmico. A figura ilustra um gás dentro de um recipiente. Se considerarmos que o gás é o sistema de interesse, então o recipiente será a fronteira deste sistema e todo o resto será considerado vizinhança. - Estado termodinâmico
- O estado termodinâmico de um sistema é caracterizado pela condição desse sistema, no caso, sua energia interna. O estado termodinâmico é caracterizado por um conjunto de grandezas macroscópicas chamadas de variáveis de estado (pressão, volume, temperatura, número de moles, etc). Quais variáveis são necessárias para determinar a energia interna do estado de um sistema são obtidas experimentalmente.
- Transformação
- Quando há uma alteração do estado do sistema, dizemos que houve uma transformação. O modo como o sistema chegou a esta alteração é denominado "processo".
- Energia interna
- É a soma das energias cinéticas de todas suas partículas constituintes acrescida da soma de todas as energias potenciais decorrentes das interações entre as partículas do sistema. (Obs.: A energia interna não inclui a energia potencial decorrente entre o sistema e suas vizinhanças.) A variação de energia interna de um gás ideal não depende do processo, depende apenas da temperatura inicial e final do mesmo.
- Energia externa
- É a trocada pelo sistema com o meio externo, nas formas de calor e de trabalho e dependem do processo de transformação, ou seja, não é intrínseca do sistema.
- Função de estado
- São funções cujos valores dependem apenas de variáveis de estado, isto é, variáveis que dependem apenas do estado de equilíbrio termodinâmico atual do sistema.
-
1ª lei da termodinâmica
- A primeira lei é essencialmente uma extensão do princípio da conservação da energia, a fim de incluir sistemas onde existe fluxo de calor. Historicamente ela marca o reconhecimento do calor como uma forma de energia (experiência de Joule). A primeira lei se aplica a todo e qualquer processo natural que decorre entre estados de equilíbrio.
- Definição da lei:
- Quando uma quantidade de calor \(Q\) é fornecida a um sistema durante um processo, parte dele \(\Delta U\) fica no sistema sob forma de energia interna e parte \(W\) deixa o sistema em forma de trabalho realizado pelo sistema sobre a sua vizinhança. Matematicamente, temos: $$\Delta U = Q - W.$$
-
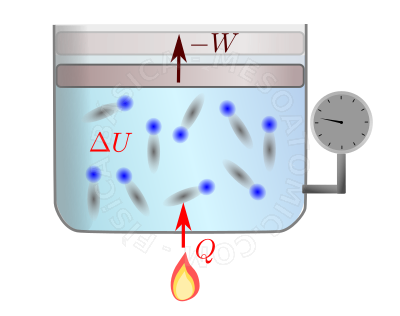
Primeira Lei da Termodinâmica. A figura ilustra um gás sendo aquecido por uma chama e expandindo (a seta superior ilustra o deslocamento do êmbolo do recipiente). Ao receber energia térmica (calor) as moléculas do gás ficam mais agitadas ( \(\Delta U\) aumenta), com isto há mais colisões entre o gás e o êmbolo, fazendo ele (o êmbolo) subir. Para o êmbolo se mover, é necessário que o gás realize trabalho sobre ele, perdendo assim alguma energia, mas, por outro lado, o embolo realiza trabalho sobre a vizinhança do sistema (no caso, no gás/ar que envolve o sistema), cedendo assim este trabalho a regiões externas ao sistema.
Aplicações da 1ª lei da termodinâmica
Dependendo da transformação que uma sustância sofre, o calor específico (e a capacidade térmica) da substância muda. Para tratar a transformação termodinâmica de um gás ideal, necessitamos considerar o calor específico a pressão constante \(c_p\) e a volume constante \(c_v\) . E é possível relacionar estas duas quantidades:
- Coeficiente de Poisson
- é possível relacionar as capacidades térmicas, ou calor específicos $$\gamma = \frac{C_p}{C_v} = \frac{c_p}{c_v}.$$ Temos os seguintes valores para \(\gamma\) :
\(\frac{5}{3} = 1,67\) para gases monoatômicos
\(\frac{7}{5} = 1,40\) para gases diatômicos, que com boa aproximação também se aplica ao ar. - Relação de Mayer:
- $$c_p - c_v = R,$$ onde \(c_p\) é o calor específico a pressão constante e \(c_v\) é o calor específico a volume constante.
Veremos agora as transformações gasosas.
- Transformação cíclica
- Numa transformação cíclica, o sistema volta sempre exatamente ao seu estado inicial, portanto: $$\Delta U = 0,$$ $$W = Q.$$
- Transformação isocórica
- São transformações a volume constante ( \(V = C^{te}\) ). O calor trocado é dado por $$ Q = m c_v \Delta T,$$ o trabalho realizado $$ W = 0,$$ e a variação da energia interna é $$ \Delta U = m C_v \Delta T,$$ onde \(m\) é a massa do gás e \(\Delta t\) a variação na temperatura.
Ex: panela de pressão - Transformação isobárica
- Transformações a pressão constante ( \(P = C^{te}\) ). Quando este processo ocorre, o calor trocado e o trabalho efetuado são, ambos, diferentes de zero. O trabalho efetuado é igual ao produto da pressão pela variação de volume, $$W = P \Delta V.$$ Como o calor trocado é $$Q = m C_p \Delta T,$$ temos $$\Delta U = m C_p \Delta T - P \Delta V$$ Ex: Processos a céu aberto são a pressão constante e atmosférica.
- Transformação isotérmica
- Transformações a temperatura constante ( \(T = C^{te}\) ). $$\Delta U = 0 \Rightarrow Q = W $$ $$W = n R T \ln \left(\frac{V_f}{V_i}\right)$$
- Transformação adiabática
- Transformação onde não há troca de calor com o meio externo \((Q = 0)\) . O trabalho desta transformação é: $$\Delta U = -W = m C_v \Delta T.$$ Ex: Reações rápidas, onde não há tempo suficiente para que haja troca de calor significativa ou quando o sistema está isolado termicamente do meio externo, através de fronteiras adiabáticas.
- Expansão livre adiabática
- A energia interna inicial e final de um gás são iguais, quando o gás sofre uma expansão livre adiabática. $$T_i = T_f$$ $$p_i \cdot V_i = p_f \cdot V_f$$
- Processo de ebulição
- Suponhamos que um líquido, de massa m, seja vaporizado à pressão constante P. O volume do líquido, é \(V_l\) , e o volume no estado de vapor \(V_v\) . $$W = P (V_f - V_i)$$ $$\Delta U = Q - W = m L_v - P (V_f - V_i)$$
