- Termofísica
- /
- Termodinâmica
- /
- Estudo dos Gases
"O universo é modelado como um gás."
Visão macroscópica dos gases
Os gases são fluidos desprovidos de forma própria, facilmente compressíveis e tendem a ocupar todo o volume do recipiente que os contém. Numa visão microscópica idealizada, temos que:
- Os gases são constituídos de moléculas.
- As forças de atração entre as moléculas do gás podem ser desprezadas.
- O volume ocupado pelas moléculas do gás é desprezível, quando comparado com o do recipiente que o contém.
- O movimento das moléculas de gás é continuo e aleatório.
Um modelo dos gases reais: o gás ideal
Para estudarmos os gases reais lançamos mão de um modelo idealizado chamado de gás ideal, que modela bem um gás real de difícil liquefação, em baixa pressão e em alta temperatura. Para o estudo dos gases é muito importante o seguinte:
- A Lei de Avogadro
- que diz que volumes iguais de gases, nas mesmas condições de temperatura e pressão, possuem o mesmo número de moléculas. Como o número de moléculas de um gás é um número muito grande, nos referimos ao número de moléculas como um múltiplo de um número muito grande chamado mol . Assim como uma dezena contém 10 unidades e uma dúzia contém 12 unidades, basta pensar no mol como "um dúzia um pouco maior".
- 1 mol de qualquer gás
- a temperatura de 0 ºC e a pressão de 1 atm ocupa o volume de 22,4 litros e contém \(6,023 \times 10^{23}\) moléculas.
- Número de Avogadro \((N_0)\)
- é o número, $$N_0 = 6,023 \times 10^{23},$$ que facilita a comunicação e a escrita do número de moléculas em um gás. É muito mais fácil dizer que em um cilindro de gás há 1 mol do que dizer que há 602.300.000.000.000.000.000.000 moléculas.
- C.N.T.P. - Condições Normais de Temperatura e Pressão
- se refere a temperatura de 0 ºC e pressão de 1 atm.
Equação de estado de um gás ideal
Cada estado de equilíbrio em que um gás se apresenta é caracterizado, do ponto de vista macroscópico, pelas seguintes propriedades macroscópicas:
- pressão \((P)\) ,
- volume \((V)\) ,
- temperatura \((T)\) .
Em um gás ideal, as variáveis acima são relacionadas através da equação de estado: $$P V = n R T,$$ onde \(n\) é o número de mols do gás e \(R\) é a constante universal dos gases perfeitos e vale $$R = 0,082 ~ atm \cdot l/mol \cdot K \\ = 8,31 ~J/mol \cdot K.$$
É extremamente importante notar que esta equação não tolera outra escalas de temperatura, apenas temperaturas em Kelvin podem ser usadas. Caso tenhamos medidas em Celcius ou Fahrenheit, precisamos primeiramente transformar para Kelvin.
Lei geral dos gases perfeitos
A lei dos gases perfeitos nos ajuda a calcular o que ocorrerá apos uma transformação ser efetuada no gás, veja a figura abaixo.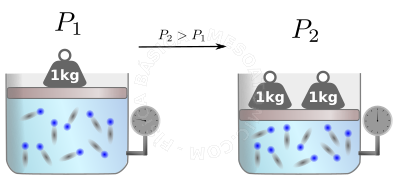
Transformações gasosas
Os gases sofrem transformações de estado quando produzem trabalho numa máquina, isto é, passam de um estado inicial para um estado final. Estas transformações podem ocorrer de diversas maneiras, algumas delas são:
- Transformação isobárica
- ocorre a pressão constante, logo \(P_1 = P_2 \Rightarrow \frac{V_1}{T_1} = \frac{V_2}{T_2}\) ;
- Transformação isotérmica
- ocorre a temperatura constante, logo \(T_1 = T_2 \Rightarrow P_1.V_1 = P_2.V_2\)
- Transformação isocórica (isovolumétrica)
- ocorre a volume constante, logo \(V_1 = V_2 \Rightarrow \frac{P_1}{T_1} = \frac{P_2}{T_2}\)
- Transformação Adiabática
- ocorre sem que aconteça trocas de calor entre o gás e o meio, logo \(Q_1 = Q_2\)
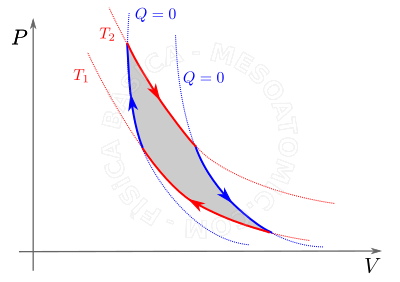
Trabalho nas transformações gasosas
Diferente do que é estudado em mecânica, o trabalho de um gás depende do estado inicial, do estado final e também dos estados intermediários. Os trabalhos realizados pelos gases em diferentes transformações são descritos a seguir.
- Transformação isobárica ( \(P = C^{te}\) )
- O trabalho \(W\) realizado por uma massa gasosa, numa transformação isobárica ( \(P = \text{Constante}\) ), que teve uma variação de volume \(\Delta V = \text{volume final} - \text{volume inicial}\) é $$W = P \cdot \Delta V.$$
- Transformação qualquer
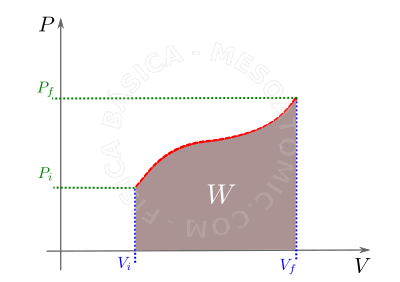
- O trabalho realizado em uma massa gasosa durante uma transformação qualquer é numericamente igual a área sob a curva no gráfico \(P \times V\) (vide gráfico abaixo). Para diferentes transformações teremos diferentes sinais para o trabalho, tal que:
- A: Expansão \(V_f \gt V_i \Rightarrow \Delta V \gt 0 \Rightarrow W \gt 0 \) ,
- B: Compressão \(V_f \lt V_i \Rightarrow \Delta V\lt0 \Rightarrow W\lt0 \) ,
- C: Volume constante \(V_f=V_i \Rightarrow \Delta V = 0 \Rightarrow W=0 \) ,
- Transformação cíclica
- É a transformação na qual, após o seu transcurso, as condições finais de pressão, volume e temperatura são iguais as iniciais, e a área limitada pelo ciclo no diagrama \(P \times V\) mede o trabalho realizado no mesmo, veja figura abaixo.
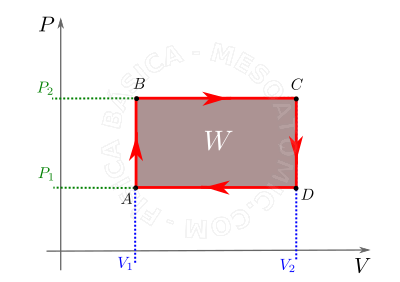
Por convenção, O trabalho realizado no ciclo é positivo se ele é percorrido no sentido horário, e negativo se é percorrido no sentido anti-horário.
