- Termofísica
- /
- Temperatura
- /
- Dilatação dos Sólidos
Dilatação térmica é o fenômeno onde a variação do volume de um corpo é ocasionada pela variação de sua temperatura, em geral, isto ocorre devido ao aumento no grau de agitação de suas moléculas e com isto há um aumento na distância média entre elas.
Dilatação dos sólidos isotrópicos
- Dilatação volumétrica
- Objetos nos quais as três dimensões são da mesma ordem, costumam apresentar variações significativas nas três dimensões, isto é, não é possível desprezar nenhuma variação. Alguns exemplos, são: cubos, paralelepípedos e etc. Para esta classe de objetos devemos aplicar a dilatação volumétrica, cuja fórmula é $$\Delta V = V_0 \gamma \Delta T,$$ onde \(\Delta V = V - V_0\) é a variação de volume, \(\gamma\) é o coeficiente de dilatação térmica volumétrica e \(\Delta T = T - T_0\) a variação de temperatura.
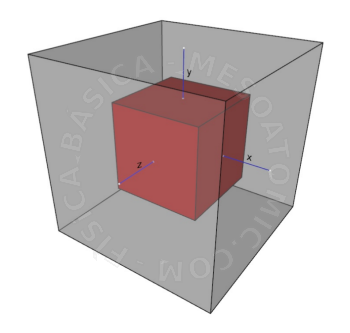
Ilustração da dilatação volumétrica. Considere o bloco vermelho na figura, aquecendo o bloco ele irá dilatar e ocupará um novo volume (bloco cinza transparente). Neste caso, o novo volume, considerando que suas dimensões duplicaram, será \(\Delta V = 2x \cdot 2y \cdot 2z\) , que é a multiplicação de toda a variação em cada dimensão. - Dilatação superficial
- Alguns objetos têm uma superfície muito grande relativamente ao seu volume. Alguns exemplos são: chapas, placas, telhas, etc. Para esta classe de objetos a variação de sua espessura costuma ser desprezível quando comparada com a superficial, de forma que a variação da área \(\Delta A\) da superfície será dada por: $$\Delta A = A_0 \beta \Delta T,$$ onde \(A_0\) é a área inicial, \(\beta\) é o coeficiente de dilatação superficial e \(\Delta T\) é a variação de temperatura que o sistema sofreu.
- Dilatação linear
- Em certas ocasiões só uma das dimensões de um objeto tem interesse prático. Quando este é o caso, estudamos somente a variação de comprimento de interesse, e não nos preocupamos com as outras duas dimensões do objeto. Um exemplo prático é a dilatação sofrida por um trilho de uma ferrovia. Embora a altura e a espessura do trilho variem, é a variação do seu comprimento que normalmente apresenta interesse, caso contrário, se não for levada em conta a dilatação do trilho durante a construção da ferrovia, esta pode acabar se deformando. No caso da dilatação linear a fórmula é $$\Delta L = L_0 \alpha \Delta T,$$ onde \(\Delta L = L - L_0\) é a variação do comprimento sofrida após uma variação de temperatura \(\Delta T = T - T_0\) , \(\alpha\) é o coeficiente de dilatação térmica linear e \(L_0\) é o comprimento do sistema antes dele sofrer uma variação de temperatura.
- Relação entre os coeficiente de dilatação para materias isotrópicos:
- $$\beta \approx 2 \alpha$$ $$\gamma \approx 3 \alpha$$ $$\beta \approx 2/3 \gamma$$
Coeficiente de dilatação linear Substância Valor ( \(10^{-6} K^1\) ) Gelo \(51\) Cobre \(17\) Aço \(11\) Vidro(comum) \(9\) Vidro (pirex) \(1,2\) Invar (ferro+níquel) \(0,7\) Quartzo fundido \(0,5\) Comentários
Do ponto de vista da dilatação, os sólidos são considerados isotrópicos quando as dilatações em diferentes direções são proporcionalmente iguais. Isto não ocorre para alguns cristais, que são chamados de anisotrópicos, que dilatam proporcionalmente mais em uma direção do que em outras.
Materiais com coeficientes de dilatação menores dilatam menos para uma mesma variação de temperatura.
Em geral, o coeficiente de dilatação varia com a temperatura, porém, em muitos casos práticos, é possível desprezar essa variação. Esta aproximação é válida quando estamos interessados em uma variação de temperatura que não seja muito grande e quando o material não se aproxime do seu ponto de fusão.
