- Óptica
- /
- Reflexão e espelhos
- /
- Espelho Plano
“O espelho testa a reflexão da luz e a irreflexão dos homens”
Gar-Mar
O Espelho Plano
É um sistema óptico estigmático, pois para cada ponto de um objeto posto na frente do espelho, é gerado apenas um ponto correspondente na imagem do espelho. Ele também conjuga, de um objeto real, imagem sempre virtual, direita e de mesmo tamanho do objeto, e há uma inversão da imagem em relação ao eixo paralelo ao espelho, mas não há inversão de cima para baixo (veja a figura abaixo). Chamamos este tipo de imagem de especular ou enantiomorfa.

- Campo Visual
- É a região do espaço que pode ser observada através do espelho.
-

Ilustração do campo visual (região cinza) de um observador em um espelho plano. - Translação de espelho
- Quando um espelho plano é deslocado paralelamente à sua posição inicial, a imagem de um objeto fixo sofre um deslocamento que é o dobro do deslocamento do espelho, no mesmo sentido.
-
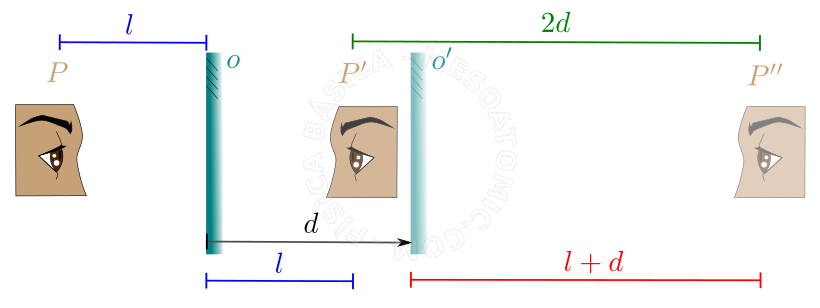
Deslocamento de um espelho plano. Para um objeto no ponto \(P\) e um espelho na posição \(o\) , uma imagem no ponto \(P'\) é gerada. Se o espelho for transladado da posição \(o\) para \(o'\) , a imagem irá passar do ponto \(P'\) para o ponto \(P''\) . Como o espelho foi transladado de uma distância \(d\) , a imagem será transladada de uma distância \(2d\) . - Rotação de espelho
- Se um espelho plano sofre uma rotação de um ângulo \(\alpha\) em torno de um vértice do espelho, o raio refletido sofre uma rotação de \(2 \alpha\) .Este resultado é deduzido usando as leis da reflexão e geometria plana (veja figura abaixo).
-
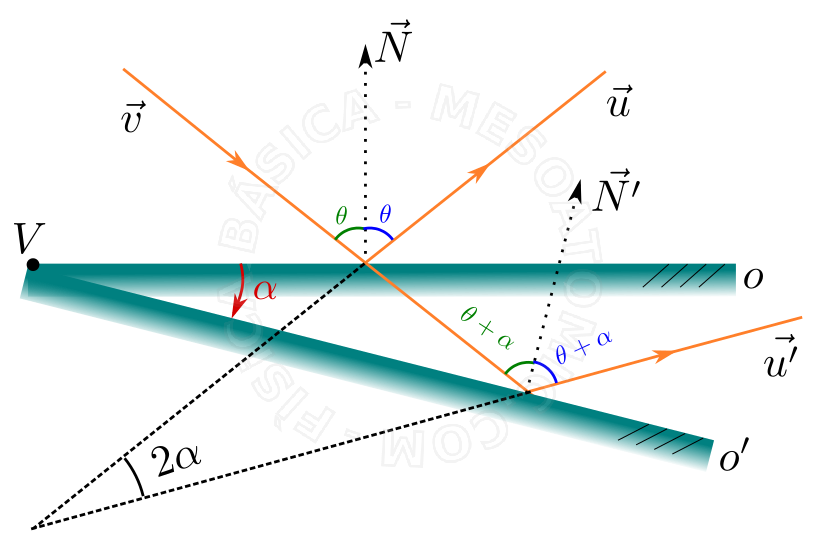
Rotação de um espelho plano. Considere um raio incidente \(\vec{v}\) em um espelho plano \(o\) que tem raio refletido \(\vec{u}\) . Se rotacionarmos o espelho de um ângulo \(\alpha\) , em relação ao vértice \(V\) , para a posição \(o'\) , o raio transmitido \(\vec{u}\) será rotacionado de \(2 \alpha\) , assumindo a direção \(\vec{u'}\) . - Associação de Espelhos Planos
- Se associarmos dois espelhos planos, de maneira que eles tenham um ângulo \(\alpha\) entre eles, teremos \(n\) imagens para um objeto \(P\) situado entre os espelhos, tal que: \begin{equation} n=\frac{360}{\alpha}-1, \end{equation} onde \( 0^o \lt \alpha \lt 180^o\) , e a expressão só é válida para valores de \(\alpha\) que sejam divisores de \(360\) , por exemplo, \(120^{o}\) , \(90^{o}\) , \(72^{o}\) . etc. Quando \(\frac{360}{\alpha}\) for um número inteiro ímpar, a expressão só é válida para um objeto situado na linha bissetora do ângulo \(\alpha\) .
-

Associação de dois espelhos com ângulo reto entre eles ( \(\alpha = 90^o\) ). Neste caso temos \(n = \frac{360}{90} - 1 = 3\) imagens.
