Interferência

É a combinação de duas ou mais ondas que se encontram na mesma região do espaço gerando uma onda resultante.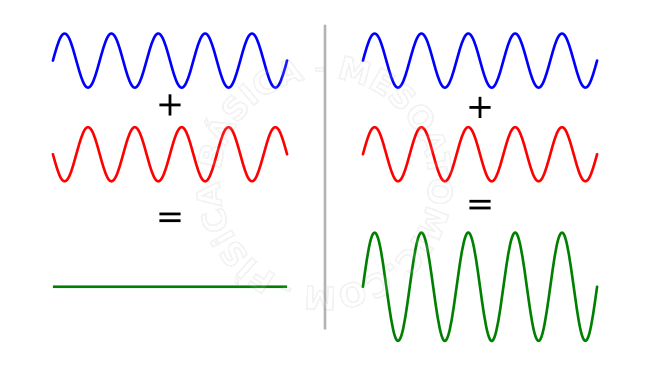

ANIMAÇÃO

Ondas estacionárias

Uma onda estacionária ocorre, quando duas ou mais ondas, em sentido opostos, formam uma única onda. Nesta onda, certos pontos não se movem. A palavra "estacionária" faz referência a estes pontos e não a onda como um todo, que vibra normalmente fora deste pontos. A distância entre dois nós ou ventres consecutivos vale \( \frac{\lambda}{2} \)

Este fenômeno pode ser observado em uma corda onde uma de suas extremidades está presa e a outra vibra. O pulso gerado pela vibração, ao viajar pela corda, quando chega a extremidade fixa é refletido de volta. A soma da onda enviada com a refletida é que pode formar uma onda estacionária, dependendo das características desta onda, veja a figura.

ANIMAÇÃO

Ondas estacionárias em tubos

Em tubos, onde uma de suas extremidades pode estar fechada ou não, onde se aplica uma onda sonora (onda de pressão no ar), também é possível obter ondas estacionárias, de modo que:

Tubos abertos

\( f_n = \frac{nv}{2L} \)

Tubos fechados

\( f_n = \frac{nv}{4L} \)

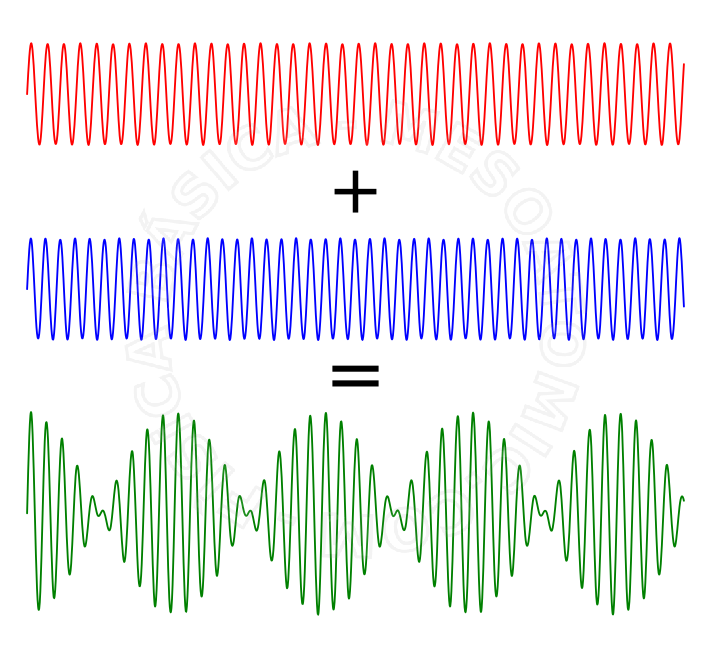
Batimentos

O batimento é o fenômeno que resulta da superposição de duas ondas de frequências ligeiramente diferentes. O batimento é uma pertubação de amplitude variável cuja frequência é igual à diferença entre as frequências das duas ondas, ou seja, o número de batimentos por segundo é igual á diferença entre as frequências das ondas componentes: \( f_{bat} = ~ ∣f_1-f_2∣.\)