- Ondulatória
- /
- Mov. harmônico simples
- /
- Osc. harmônico e Pêndulo Simp.
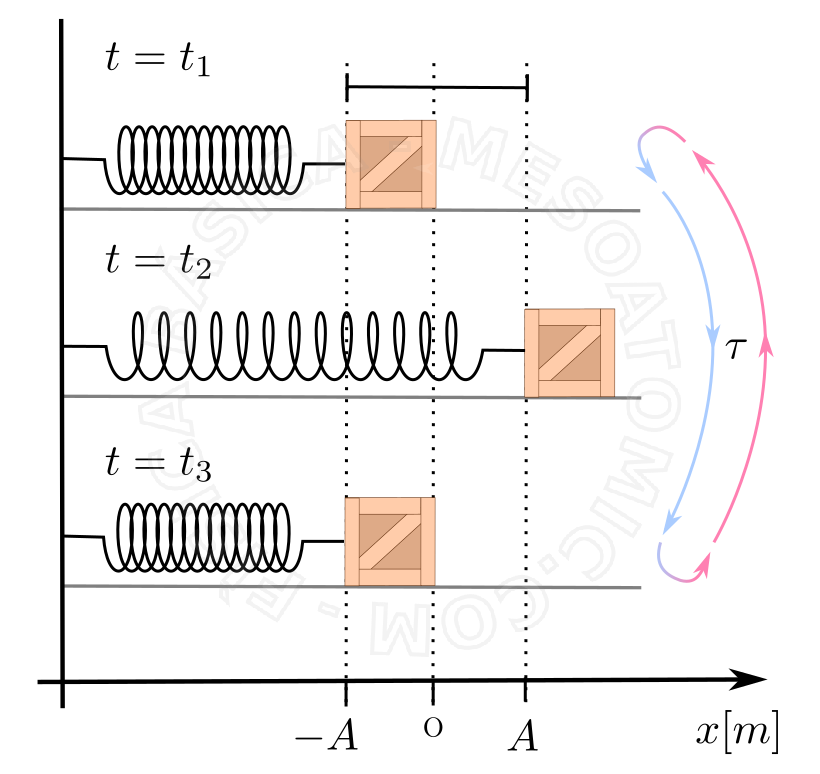
O oscilador harmônico simples é um sistema isolado de forças externas, além de não ter amortecimento algum. Ele também é conhecido como sistema massa-mola. Neste sistema, a única força que age é a elástica da mola.
Oscilador Harmônico Simples
Temos para este sistema as seguintes características:
- 1. O corpo preso à mola executa o movimento harmônico simples (MHS)
- 2. A elongação no MHS é, em módulo, a própria deformação (distensão ou contração) da mola.
- 3. A força resultante no corpo é a própria força elástica aplicada pela mola, quando a força peso e normal são perpendiculares ao movimento e o atrito é desprezível.
- 4. No ponto de equilíbrio, a força elástica (força resultante) é nula e a mola não está deformada.
Energia
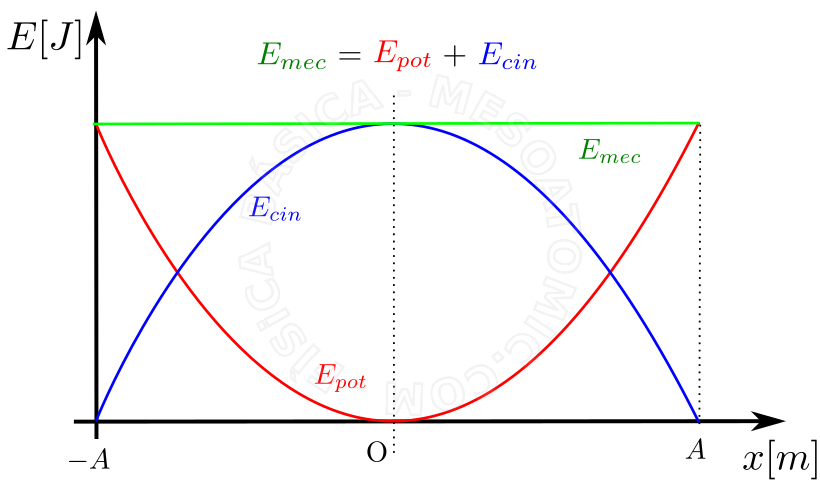
Dado um sistema massa-mola ou outro oscilador harmônico simples, onde as forças de atrito são desprezadas, haverá conservação de energia mecânica, isto é, para qualquer configuração do sistema a soma da energia cinética mais a potencial é constante. No caso do sistema massa-mola, temos:
- \( E_c = m \frac{v^2}{2} \)
- \( E_{el} = \frac{k x^2}{2} \)
- \( E_{mec} = E_c + E_{el} = \frac{k A^2}{2} = C^{te} \)
- \( E_{el} = \frac{k x^2}{2} \)
Associação de molas
Imagine que temos dois corpos A e B e queremos prender mais de uma mola entre eles. Chamamos de "Associação em série" quando juntamos as molas uma após a outras, em fila. Já em paralelo, cada mola está ligada entre A e B.
No cálculo, podemos substituir todas as constantes elásticas por uma equivalente, dependendo da configuração:
- Série
- \( \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} \)
- Paralela
- \( k_{eq} = k_1 + k_2 \)
O pêndulo simples
É um dispositivo constituído por uma partícula de massa \(m\) suspensa por uma haste (corda ou fio) de massa desprezível e comprimento \(L\) . Em relógios antigos (relógios de caixa alta) pêndulos simples são utilizados para marcar a passagem do tempo. O pêndulo se comporta como um oscilador harmônico quando a amplitude de vibração do mesmo é pequena em relação a vertical (pequenos ângulos).
Período de um pêndulo simples
Considerando o atrito desprezível, através das leis de Newton é possível deduzir o período do pêndulo simples para pequenos ângulos, que é: $$ \tau = 2 \pi \sqrt{\frac{L}{g}},$$ onde \(g\) é a aceleração da gravidade e \(L\) é o comprimento do pêndulo. Este período tem as seguintes propriedades:- Só depende do comprimento da haste e da aceleração da gravidade local
- Não depende da massa pendular
- É isócrono, isto é, o período não depende da amplitude.
- Não depende da massa pendular

