- Ondulatória
- /
- Mov. harmônico simples
- /
- MHS: Conceitos Básicos
Na natureza encontramos com frequência fenômenos que se repetem continuamente. As estações do ano, as fases da lua e os nossos batimentos cardíacos, são exemplos destes fenômenos. O movimento harmônico simples (MHS) é um modelo que serve para descrever diversos fenômenos deste tipo, logo, todo movimento harmônico simples é periódico e oscilatório.
Conceitos básicos
- Def. 1
- É o movimento executado por uma partícula sujeita a uma força proporcional ao deslocamento e de sinal contrário. A força no MHS é do tipo: \( F \propto x \) , sendo \(x\) o deslocamento em relação a posição de equilíbrio. Notação: O símbolo " \(\propto\) " denota proporcionalidade.
- Def. 2
- Chama-se MHS a todo movimento que obedece a uma lei representada por uma função senoidal (ou cossenoidal) do tipo: $$ x = A sen(\omega t + \theta_0)$$ ou $$ x = A cos(\omega t + \theta_0)$$
- Movimento periódico
- é todo movimento onde uma mesma situação se repete em intervalos de tempo iguais.
- Movimento Oscilatório (vibratório)
- Todo movimento simétrico em torno de um ponto de equilíbrio.
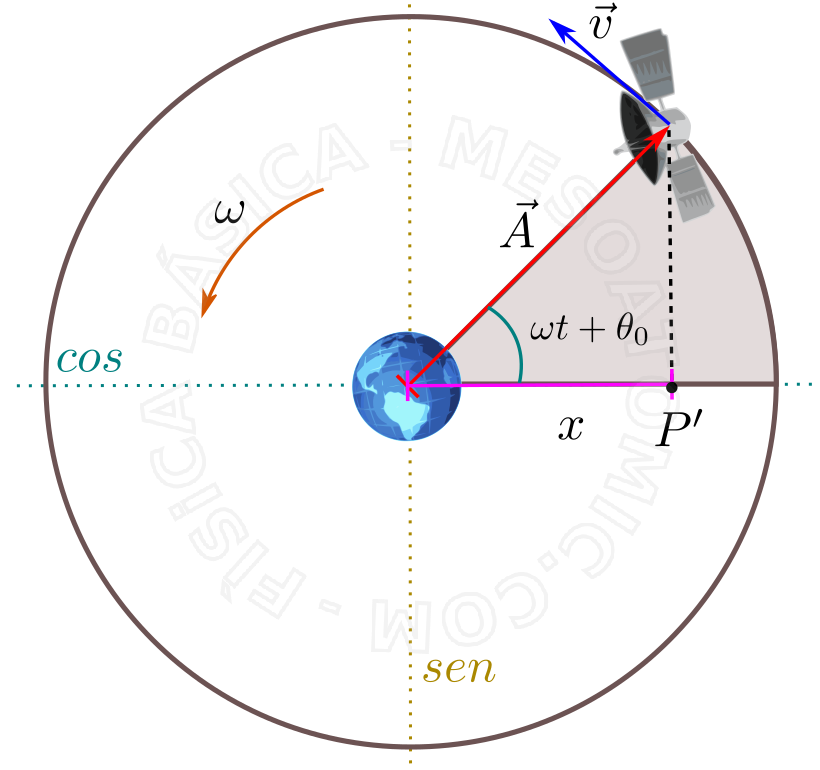
Funções horárias do MHS:
- Amplitude ( \(A\) )
- do MHS é a medida do deslocamento da origem do sistema até o ponto máximo.
- Fase inicial ( \(\theta_0\) ):
- é o desvio do corpo em relação a posição de equilíbrio no tempo inicial, \(t = 0\) .
- Velocidade angular ( \(\omega\) ):
- é a "pulsação" ou frequência angular do movimento. Que é dado por $$ \omega = \frac{2 \pi}{\tau} = 2 \pi f,$$ onde \(\tau\) é o período e \(f\) a a frequência do movimento.
- Elongação ( \(x\) )
- é o distânciamento do sistema ao ponto de equilíbrio, e é dado por $$x = A cos ( \omega t + \theta_0 ).$$
- Velocidade ( \(v\) )
- \(v = -\omega A sen ( \omega t + \theta_0 )\)
- Aceleração ( \(a\) )
- \(a = -\omega^2 A cos ( \omega t + \theta_0 )\)
- Velocidade em função da elongação:
- \(v = \omega^2 (A^2- x^2) \)
- Velocidade nos pontos de inversão:
- \(v = 0 \)
- Velocidade no ponto central:
- \(v = \pm \omega^2 x \) (máx e mín)
- Aceleração em função da elongação:
- \(a = -\omega^2 x \)
- Aceleração no ponto de inversão:
- \(a = \pm \omega^2 A \) (máx e mín).
- Aceleração no ponto central:
- \(a = 0 \)
