- Mecânica
- /
- Estática
- /
- Estática dos Sólidos
Existem duas formas simples de movimentos para um sistema rígido: translação e rotação. Qualquer outra forma de movimento possível, por mais complexa que seja, pode sempre ser considerada como a superposição de uma rotação e uma translação.
Estática dos Sólidos
Nem sempre é possível considerar um corpo como uma partícula pontual, em geral, quando estamos interessados não só no deslocamento de um objeto, mas também em sua rotação, a seguinte definição é importante:
- Corpo rígido ou sólido
- O modelo adotado para objetos extensos considera que o tamanho e a forma destes praticamente não se alteram quando submetidos a forças externas, apesar das ligações moleculares reais não serem perfeitamente rígidas. Pontes, aviões e muitos outros objetos podem ser considerados bons exemplos de corpos rígidos, estes se deformam pouco, e, sobre a ação de forças muito intensas, se quebram.
Os dois possíveis tipos de movimento de um corpo rígido podem ser definidos como:
- Translação
- É o movimento onde se modifica a posição de um objeto, ou seja, todos os pontos do corpo são movidos de uma distância fixa em uma mesma direção.
- Rotação
- No movimento de rotação todos os pontos do corpo se movem em arcos de circunferências, cujos centros estão no mesmo eixo, chamado de eixo de rotação.
Equilíbrio dos sólidos
Para que um sólido esteja em equilíbrio num referencial inercial, é necessário satisfazer duas condições: uma referente ao equilíbrio de translação e outra referente ao equilíbrio de rotação, definidas a seguir:
- Equilíbrio de translação
- A condição de equilíbrio de translação de um corpo rígido é que o centro de massa esteja em repouso ou em movimento retilíneo e uniforme, ou seja, que a resultante das forças externas atuantes no corpo seja nula. De forma matemática: $$\vec{F}_r = \vec{0}$$ onde \(\vec{F}_r\) é a resultante das forças no sistema.
- Equilíbrio de rotação
- A condição de equilíbrio estático de rotação é que o corpo não rotacione. Para que isto ocorra, em um corpo rígido sob ação de um sistema de forças, é preciso que a soma dos momentos de todas as forças em relação a um eixo qualquer seja nula. De forma matemática: $$ \vec{M_r} = \vec{0},$$ onde \(\vec{M_r}\) é o torque resultante sobre o sistema.
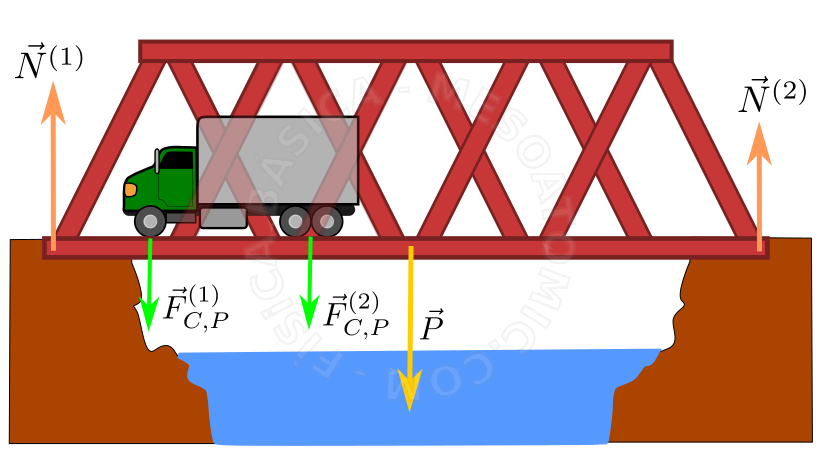
A figura a cima ilustra um corpo extenso, a ponte, sofrendo a ação de diversas forças. Considerando que o sistema de interesse é a ponte, para que esta esteja em equilíbrio estático, as forças atuando na mesma devem atender as seguintes condições: para que não haja translação a resultante deve ser zero, \begin{align} +& \vec{N}^{(1)} + \vec{N}^{(2)} + \vec{F}_{C,P}^{(1)} +\\ +& \vec{F}_{C,P}^{(2)} + \vec{P} = 0, \end{align} e para que não haja rotação, o torque sobre a ponte também deve ser zero, \begin{align} -& N^{(1)} d_{1} + N^{(2)} d_{2} + F_{C,P}^{(1)} d_{3} +\\ +& F_{C,P}^{(2)} d_{4}+ P d_{5}= 0, \end{align} onde cada \(d_i\) é a distância de cada força em relação ao centro de massa da ponte, posição do vetor \(P\) , logo, \(d_5 = 0\) .
Teorema de Lamy
Se um sistema rígido estiver em equilíbrio, sob ação de apenas três forcas externas, \(F_1\) , \(F_2\) e \(F_3\) , não paralelas, o módulo de cada uma delas é proporcional ao seno do ângulo entre as outras duas, ou seja: $$ \frac{F_1}{sen(a)} = \frac{F_2}{sen(b)} = \frac{F_3}{sen(c)},$$ onde \(a\) , \(b\) e \(c\) são os ângulos entre as forças, como ilustra a figura abaixo. 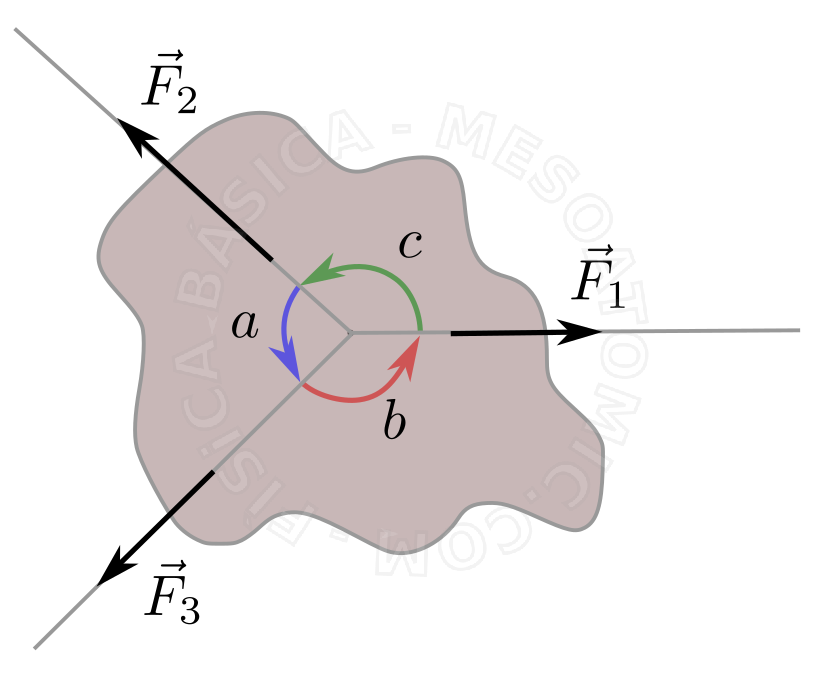
Teorema de Poisont
Qualquer sistema de forças por mais complexo que seja, sempre pode ser reduzido a uma força única, conhecida como força resultante, e a um binário, cujo plano seja ortogonal a força resultante.
