- Mecânica
- /
- Estática
- /
- Estática da Partícula
A estática é o ramo da mecânica que estuda as forças que atuam nos objetos que estão em repouso. Na engenharia civil a estática é particularmente importante na construção de prédios, pontes, viadutos e outras estruturas que devem ficar em repouso (estáticas).
Estática da Partícula
Neste estudo é importante diferenciar partícula de corpo rígido.
- Partícula
- Partícula ou ponto material é qualquer objeto cujas dimensões sejam muito pequenas, quando comparadas com as outras dimensões envolvidas no problema. Ao considerarmos um objeto como partícula, estamos supondo que os efeitos rotacionais não são importantes no estudo. Por exemplo: a Terra pode ser considerada uma partícula se estivermos estudando apenas o seu movimento em torno do sol.
- Corpo rígido
- É aquele que praticamente não sofre deformação quando sob ação das forças que atuam sobre ele. As dimensões influem na análise do seu equilíbrio, isto é, ele não pode ser tratado como partícula. Por exemplo: A prancha de uma gangorra não pode ser considerada uma partícula, pois a posição de aplicação da força(normal) que as crianças fazem na gangorra irá influenciar no equilíbrio da mesma.
- Centro de massa
- Para os casos onde é possível tratar um corpo extenso como uma partícula pontual, considera-se que toda a massa deste corpo está localizada em um ponto, este é conhecido como centro de massa ou centro de gravidade . No caso de um objeto homogêneo, este ponto é o centroide ou centro geométrico do corpo. É neste ponto que devemos desenhar o vetor peso.
Condições de equilíbrio estático de uma partícula
Da primeira lei de Newton, sabe-se que: para uma partícula em repouso permanecer neste estado, é necessário que a força resultante sobre a mesma seja zero. Matematicamente temos: $$\vec{F}_r = \sum_i^n \vec{F}_i = \vec{0},$$ onde \(\vec{F}_r\) é a força resultante e \(\vec{F}_i\) são as \(n\) forças que atuam no sistema. Podemos reescrever isto de foma explícita, em termos das componentes horizontais \(x\) e verticais \(y\) , assim obtém-se: \begin{array} \\ F_{r,x} = \sum_i^n \pm F_{i,x} =\\ = \pm F_{1,x} \pm F_{2,x} \pm ... \pm F_{n,x} = 0,\\ F_{r,y} = \sum_i^n \pm F_{i,y} =\\ = \pm F_{1,y} \pm F_{2,y} \pm ... \pm F_{n,y} = 0, \end{array} onde \(F_{r,x}\) e \(F_{r,y}\) são os valores algébricos das componentes horizontais e verticais da força resultante , ou seja, o módulo da força acompanhada do sinal algébrico que indica o sentido da mesma. Respectivamente, \(F_{i,x}\) e \(F_{i,y}\) são os módulos das componentes das forças que atuam no sistema , e o sinal \((\pm)\) a frente do módulo, deve ser escolhido conforme o sentido da componente da força em questão.
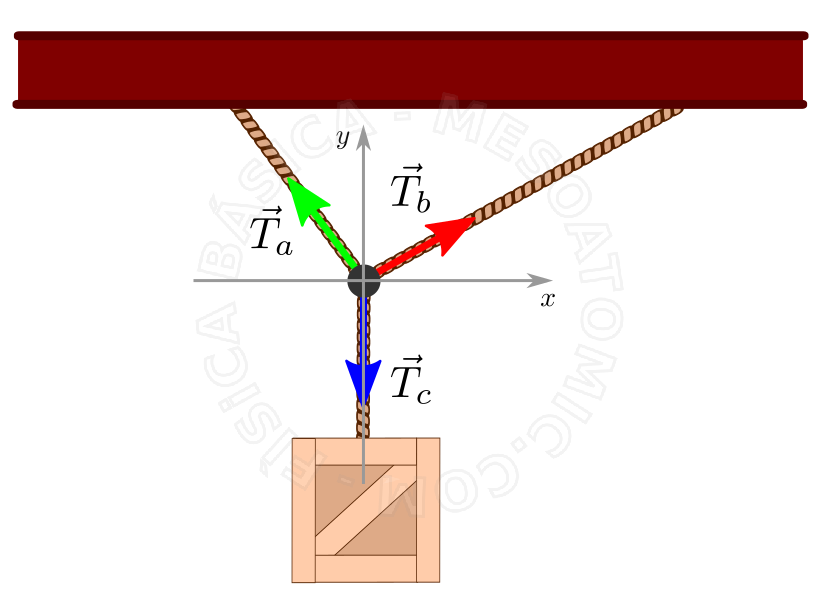
A figura acima ilustra um problema onde é possível considerar o corpo, que no caso é o nó entre as cordas, como uma partícula pontual. Neste caso a força resultante é: $$ \vec{F}_r = \sum_i^n \vec{T}_i = 0,$$ ou, de forma explícita: \begin{array} \\ F_{r,x} &= -T_{a, x} + T_{b,x} + 0 = 0,\\ F_{r,y} &= +T_{a, y} + T_{b,y} - T_{c,y} = 0. \end{array}
