- Mecânica
- /
- Estática
- /
- Centro de Massa
Centro de massa é o ponto de um sistema de partículas que se move como se todas as massas e forças externas estivessem nele concentradas.
Centro de Massa
A determinação do centro de massa é feita através da média ponderada: \begin{array} \\ X_{cm} &=\frac{m_1 x_1+m_2 x_2 +...+ m_n x_n}{m_1+m_2+...+m_n},\\ Y_{cm} &=\frac{m_1 y_1+m_2 y_2 +...+ m_n y_n}{m_1+m_2+...+m_n}, \end{array} onde o fator ponderante \(m_i\) é a massa da \(i\) -ésima partícula e \((x_i,y_i)\) é a sua posição, como ilustra a figura abaixo. 
- O centro de massa de um sistema isolado, ou seja, onde a resultante das forças é igual a zero, move-se em movimento retilíneo e uniforme , MRU, num referencial inercial qualquer.
- O centro de massa de um sistema de partículas move-se como se fosse uma única partícula , sujeita as mesmas forças do sistema como um todo. Neste caso, considera-se que a massa total do sistema está concentrada nesta única partícula.
- A quantidade de movimento total de um sistema é igual ao produto da massa total pela velocidade do centro de massa.
- O centro de massa de um sistema que apresenta distribuição uniforme de massa é o próprio centro geométrico (centróide) .
Distribuição Contínua
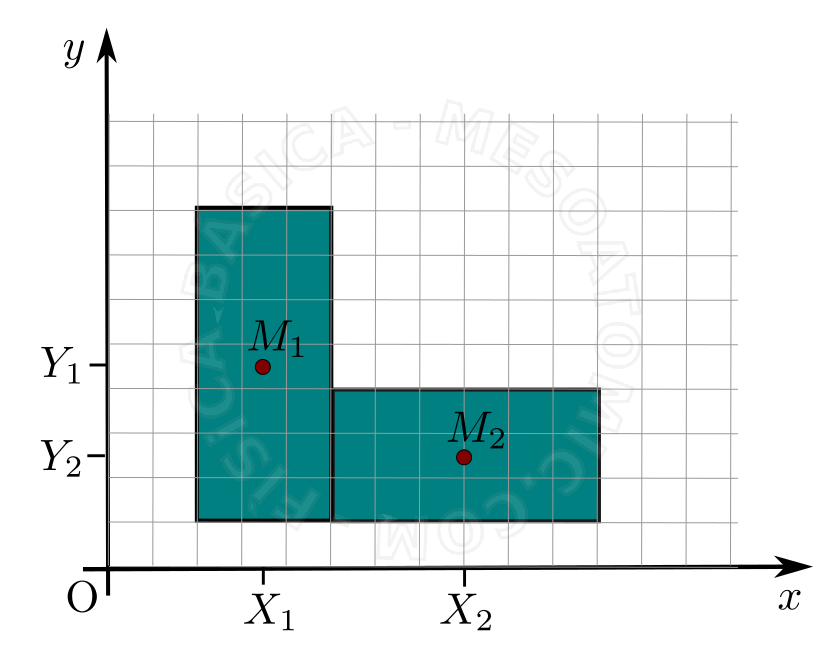
Para o caso de um corpo contínuo, como ilustra a figura acima, é possível simplificar o cálculo se considerarmos que o corpo é composto por dois retângulos onde a distribuição da massa é homogênea. Neste caso, o centro de massa de cada retângulo estará no seu respectivo centróide e o centro de massa do sistema como um todo, os dois retângulos, pode ser calculado com as fórmulas: \begin{align} X_{CM} &= \frac{X_1 M_1 + X_2 M_2}{M_1 + M_2},\\ Y_{CM} &= \frac{Y_1 M_1 + Y_2 M_2}{M_1 + M_2}, \end{align} onde \((X_1, Y_i)\) é a posição do centro de massa do objeto de massa total \(M_i\) .
