- Mecânica
- /
- Dinâmica
- /
- Leis de Newton
Uma vez que se conheça as forças que atuam em um objeto, é possível usar as leis de Newton para entender se o corpo entrará em movimento e as características desta dinâmica.
Para aplicação das leis apresentadas a seguir, é necessário que o observador do sistema esteja em um referencial inercial, ou seja, que ele esteja parado ou em movimento retilíneo uniforme. Referenciais acelerados exigem uma outra formulação. Em um primeiro momento, para facilitar, considera-se apenas que o corpo pode se movimentar sem girar (movimento de translação). Não podemos com esta formulação, por exemplo, considerar o movimento de uma bola que ao se deslocar também rotaciona. Por tanto, dizemos que o corpo sob análise é tratado como uma partícula.
Leis de Newton
- \(1^a\) - Lei da inércia
- Se a força resultante que atua em um corpo é nula, este corpo só pode estar em repouso ou movimento retilíneo uniforme (MRU).
A lei da inércia pode parecer pouco intuitiva num primeiro momento. Na Terra, os corpos só permanecem em movimento quando há atuação de forças que superam as de atrito. Não se observa algo que se movimenta eternamente sem que uma força esteja atuando. Porém, no espaço, onde não há atrito, um corpo que não interage com nenhum outro e já se encontra em movimento, permanecerá em movimento retilíneo eternamente (MRU), como ilustra a animação acima. - \(2^a\) - Lei Fundamental da dinâmica.
- A aceleração adquirida por um corpo é diretamente proporcional a força resultante e inversamente proporcional a sua massa. Que de forma matemática, pode ser escrita como \(\vec{a} = \frac{\vec{F_r}}{m}\) , ou, de forma mais conhecida: $$ \vec{F}_r = m \vec{a},$$ onde \(\vec{F}_r\) é a força resultante que atua no sistema de interesse.
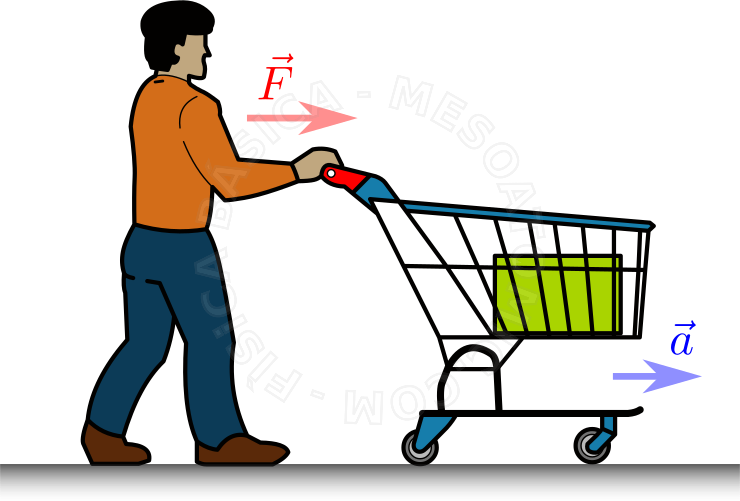
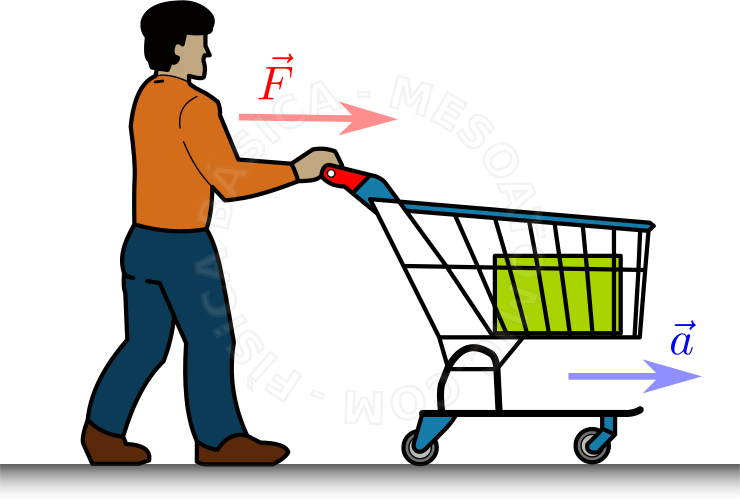

As figuras ilustram os conceitos da Segunda Lei. Considere diferentes carrinhos carregando blocos de mesmo material, onde as forças resultantes são rotuladas como \(\vec{F}\). Cada força vai gerar uma aceleração, na mesma direção da força. Ao aumentarmos a força, aumentamos a aceleração, como ilustra a segunda figura (repare no tamanho dos vetores). No entanto, se aumentarmos a massa do carrinho e aplicarmos a mesma força da segunda figura, temos uma aceleração menor. - \(3^a\) - Lei da Ação e Reação.
- Toda força aplicada gera uma força de reação de mesmo módulo e direção, porém de sentido contrário. Em forma matemática: $$ \vec{F}_{a,b} = - \vec{F}_{b,a}, $$ onde \(\vec{F}_{a,b}\) é a força que um corpo \(a\) faz em um corpo \(b.\)

Considere um nadador parado em uma piscina. Inicialmente, para ele conseguir ir para frente, ele empurra a parede para trás, e como reação, a parede empurra ele para frente. Mas como os fluidos tendem a frear objetos em movimento (força de arrasto), a tendência natural é que o nadador volte ao repouso. Mas, ao nadar, o atleta continua em movimento, pois empurrar a água para trás, e por reação, a água empurra o nadador para frente.
Forças inerciais
Forças inerciais ou fictícias são aquelas que aparecem ao adotarmos um referencial não inercial, como é o caso discutido abaixo.
A mesma situação descrita acima pode ser analisada de um referencial inercial, no caso, a estrada.
Para que um móvel descreva uma trajetória circular, a aceleração dele precisa ter módulo \(\frac{v^2}{r}\), como foi discutido na seção de movimento circular. Logo, a resultante centrípeta é \(F_c = m \frac{v^2}{r}\). Note que a resultante nunca é representada no diagrama de forças, logo, a força centrípeta nunca deve ser representada num diagrama de forças.
