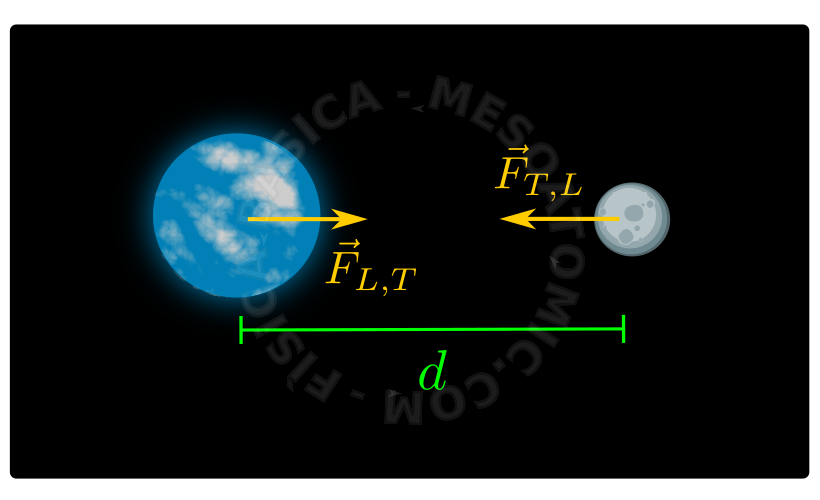
Considerando as duas massas representadas na figura acima: uma de massa \(M\) e outra de massa \(m\) , separadas por uma distância \(d\) , ocorrerá entre elas atração gravitacional cuja intensidade é: $$ F = G\frac{ M m }{d^2},$$ onde \(G\) é uma constante de módulo \(6.67 \times 10^{-11} N(\frac{m}{kg})^2\) . A direção desta força é dada pela reta que liga o centro de massa dos objetos, já o sentido, é de um objeto para o outro, como ilustra a figura.

Leis de Kepler

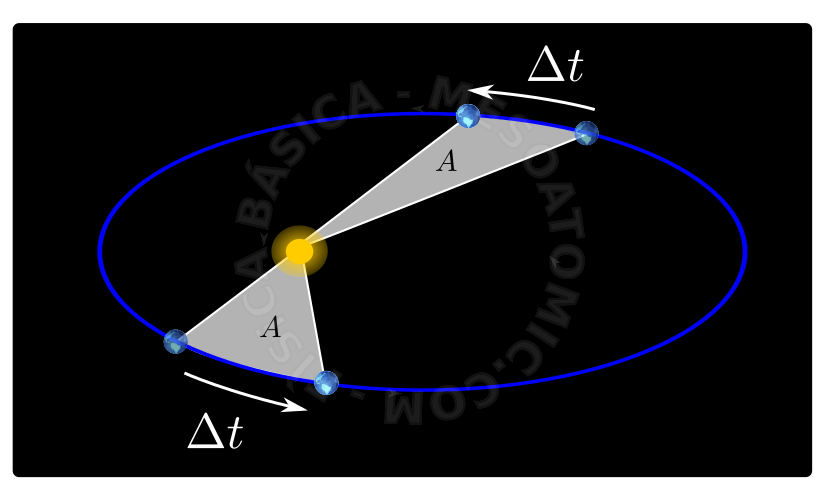
Devido a atração que os corpos celestes exercem entre si, as seguintes leis foram descobertas por Kepler:

\(1^a\) - Lei das órbitas

Os planetas descrevem trajetórias elípticas, onde o Sol ocupa um dos focos da elipse.

\(2^a\) - Lei das áreas

A área varrida pelo raio vetor de um planeta preenche áreas iguais em tempos iguais (veja a figura acima).

\(3^a\) - Lei dos períodos

Os cubos dos raios médios dos planetas em torno do Sol são proporcionais aos quadrados dos períodos de revoluções. Ou de forma matemática: $$ R^3 = k \tau^2,$$ onde \(R\) é o raio médio, \(\tau\) é o período de rotação em torno do Sol e \(k\) é uma constante. Você pode encontrar na literatura esta fórmula escrita de outras maneiras, que são equivalentes, como $$ \tau^2 = k'R^3,$$ onde \(k' = \frac{1}{k}\) é também uma constante.

Obs: Quanto mais afastado um planeta estiver do Sol (maior o raio), maior será o seu período de rotação em torno do Sol(maior será o \(\tau\) ).