- Mecânica
- /
- Cinemática
- /
- Movimentos Básicos
Considere um carro que está vazando óleo, de forma que o óleo pinga em intervalos de tempos iguais. As posições das marcas de óleo na pista podem ser usadas para entender o movimento deste carro. Na animação abaixo, veja o que acontece se fizermos um gráfico do momento em que a gota de óleo caiu, \(t\), versus a posição, \(s\). Experimente os casos limites: aceleração nula e uma velocidade inicial diferente de zero; velocidade inicial nula e uma aceleração diferente de zero. (obs: a aceleração é constante durante todo o movimento)
Movimento uniforme (MU)
É o movimento no qual a velocidade escalar é constante e diferente de zero , \(v(t) = v = \mbox{constante} \ne 0 \) . A função horária da posição, ou seja, a posição como função do tempo, para este movimento é $$ s(t) = s_0 + v t.$$
A figura abaixo ilustra o gráfico \(s \times t\) deste movimento, que neste caso é sempre uma reta, que será crescente se \(v \gt 0\) e decrescente se \(v \lt 0.\)
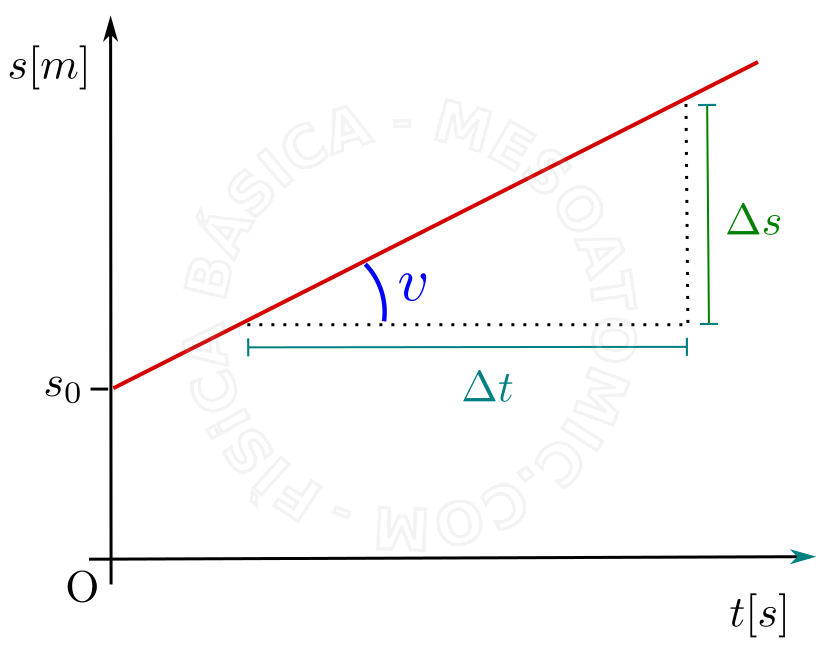
Em matemática, o coeficiente angular da reta pode ser relacionado com o ângulo que a reta faz com o eixo-x. Em física, para o MU e outros tipos de movimentos, alguns autores fazem a relação entre a tangente do ângulo que a reta faz com o eixo-x e a velocidade do movimento. No entanto, rigorosamente, esta comparação é problemática, pois tangente é uma quantidade adimensional (que não tem unidade) e velocidade tem dimensão (espaço sobre o tempo), não sendo possível relacionar diretamente estas duas quantidades. Ou seja, só é conveniente falar do ângulo que a reta faz com o eixo-x quando os eixos coordenados não tem unidades ou quando os dois eixos tem a mesma unidade.
Movimento uniformemente variado (MUV)
Movimento uniformemente variado, ou MUV, é o movimento no qual a aceleração escalar é constante e diferente de zero, \(a(t)=\mbox{constante} \ne 0\) .
As funções para este tipo de movimento são:
- Função horária da posição
- $$s(t) = s_0 + v_0 t + a \frac{t^2}{2};$$
- Função horária da velocidade
- $$v(t) = v_0 + at;$$
- Equação de Torricelli
- $$v^2 = v_0^2 +2 a \Delta s,$$ neste caso \(v\) é função de \(\Delta s\) .
Gráficos e interpretações
Os gráficos deste movimento e suas interpretações são apresentados abaixo.
- Espaço \(\times\) tempo \((a \gt 0)\)
-

- Espaço \(\times\) tempo \((a \lt 0)\)
-

- Velocidade \(\times\) tempo \((a \gt 0)\)
-
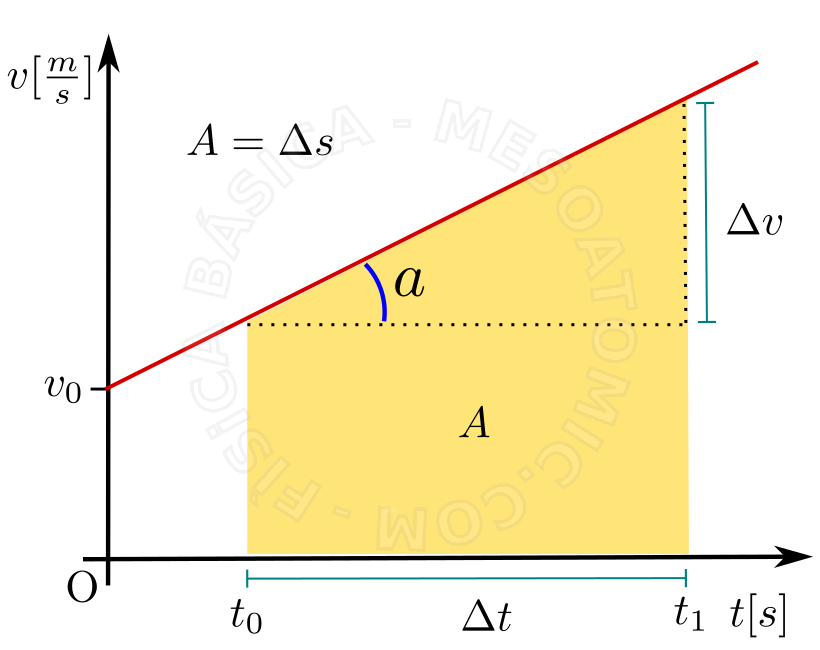
A área \(A\) sob a curva do gráfico \(v \times t \) , região amarela, é o espaço percorrido pelo móvel de \(t_0\) a \(t_1\) . Neste mesmo gráfico, a aceleração é dada pela inclinação da reta, sendo assim, se a aceleração fosse negativa, o gráfico seria uma reta inclinada para baixo.
