- Mecânica
- /
- Cinemática
- /
- Cinemática Vetorial
Quando o movimento acontece em duas dimensões ou mais, é preciso trabalhar com vetores, ou seja, é preciso usar a cinemática vetorial. Um exemplo de movimento em duas dimensões é um carro descrevendo uma trajetória circular.
Cinemática Vetorial
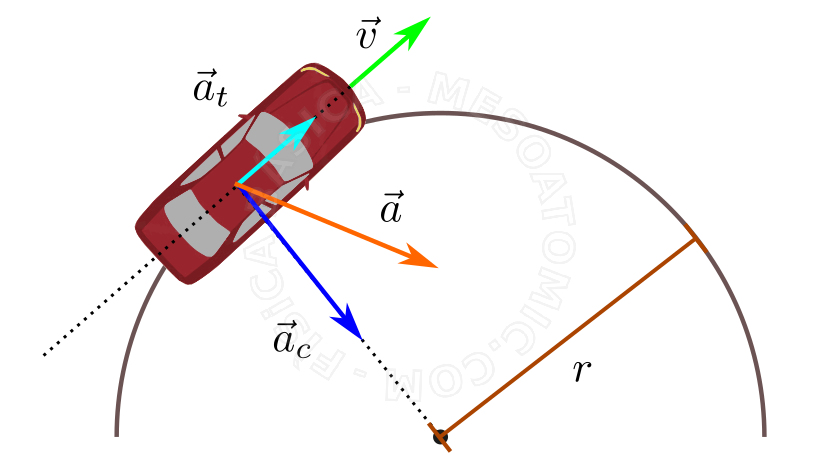
A figura acima ilustra os vetores presentes em um movimento bidimensional (trajetória circular), que podem ser entendidos da seguinte maneira:
- Vetor Velocidade \((\vec{v})\)
- O vetor velocidade tem sempre a direção da reta tangente à trajetória no ponto onde localiza-se o móvel e mesmo sentido do movimento.
- Vetor Aceleração tangencial \((\vec{a_t})\)
- É a componente da aceleração que indica a variação do módulo da velocidade e tem sempre a mesma direção da velocidade. No caso de um movimento acelerado , \( \vec{a_t} \) tem o mesmo sentido da velocidade, no caso desacelerado , \( \vec{a_t} \) tem sentido oposto à velocidade.
- Vetor Aceleração Centrípeta \((\vec{a_c})\)
- É a componente da aceleração que muda a direção da velocidade , tem direção e sentido apontando para o centro da trajetória a partir da posição do móvel. O módulo desta aceleração em um dado instante é $$ a_c = \frac{v^2}{r} $$ , onde \(v\) é o módulo da velocidade e \(r\) é o raio de curvatura da trajetória, no instante considerado.
- Vetor Aceleração Resultante \((\vec{a})\)
- É a soma de todas as acelerações que atuam no corpo. Vetorialmente \( \vec{a} = \vec{a}_t +\vec{a}_c \) , de forma algébrica \( a^2 = a_t^2 + a_c^2 \) .
