- Fluidos
- /
- Hidrostática
- /
- Princípios
Para podermos descrever o comportamento dos fluidos em diferentes situações, é importante conhecer os princípios fundamentais.
Princípio Fundamental da Hidrostática (Princípio de Stevin)
A diferença entre as pressões de dois pontos distintos dentro de um líquido em equilíbrio é proporcional a massa específica do líquido , \(\rho\) , o módulo da aceleração da gravidade, \(g\) , e as diferenças nas alturas dos pontos considerados, \(h\) , matematicamente, temos $$\Delta P = P_B - P_A = \rho g h.$$ 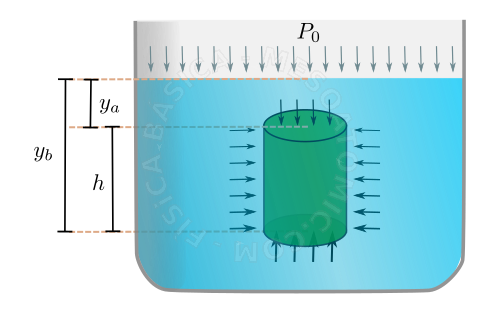
- à existência de um campo gravitacional
- ou devido a uma aceleração do fluido por forças externas (não gravitacionais)
- ou devido a uma combinação de ambas as causas.
É importante ressaltar que, no caso do ar, como a densidade é muito baixa, podemos desconsiderar a variação da pressão com a altura quando esta variação é da ordem de alguns metros.
Consequências do princípio de Stevin
- Pontos que suportam a mesma pressão pertencem a um mesmo plano horizontal. Consequência: Toda superfície livre de um líquido em equilíbrio é horizontal

Princípio dos vasos comunicantes. Não importa a geometria dos recipientes, se o líquido pode passar de um para o outro livremente, as linhas horizontais nestes recipientes apresentarão todas as mesmas pressões, as quais aumentam com a profundidade ( \(P_h \gt P_0\) ) como estabelece o princípio de Stevin. - Quando líquidos imiscíveis (aqueles que não se misturam) são colocados em um recipiente, eles se dispõem do fundo para o topo do recipiente, segundo a ordem decrescente de suas densidades; a superfície de separação entre dois líquidos não miscíveis é plana e horizontal.
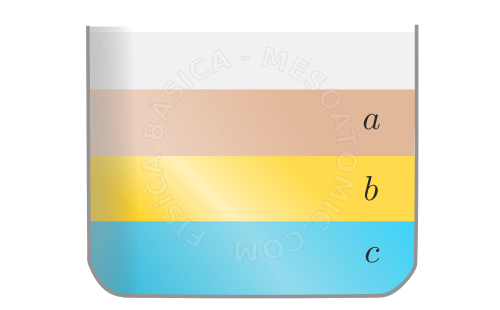
líquidos imiscíveis. A figura ilustra três líquidos que não se misturam, por exemplo, o líquido \(a\) poderia ser água, \(b\) óleo de cozinha e \(c\) álcool. - Se colocarmos dois líquidos não miscíveis num tubo em forma de "U", as alturas alcançadas pelos líquidos, contadas a partir da superfície de separação, são inversamente proporcionais as massas específicas dos líquidos, isto é $$ \frac{h1}{h2} = \frac{\rho_2}{\rho_1}.$$

líquidos imiscíveis em tubo em forma de "U". No caso, o líquido laranja tem densidade \(\rho_l\) que é menor que a densidade do líquido azul, \(\rho_a\) , por isto ele fica em cima. Apesar das superfícies em contato com o ar (superfícies livres) estarem a alturas diferentes, devido a baixa densidade do ar, é uma boa aproximação considerar que a pressão atmosférica \(P_0\) é a mesma nestes dois pontos. Com isto podemos relacionar as densidades dos líquidos com as alturas, pois \(P_0 + \rho_l g h_1 = P_0 + \rho_a g h_2\) , ou seja $$\rho_l h_1 = \rho_a h_2.$$
Lei de Pascal
Uma variação de pressão que ocorre em qualquer ponto de um líquido em equilíbrio, se transmite integralmente para todos os pontos do líquido. 
