Estudio de los gases

Termofísica
/
Termodinámica
/
Estudio de los gases

"El universo es modelado como un gas."

Vista macroscópica de los gases

Los gases son fluidos que no tienen forma propia, fácilmente compresibles y tienden a ocupar todo el volumen del recipiente que los contiene. Una vista microscópica idealizada, tenemos:

Los gases son constituidos por moléculas.
Las fuerzas de atracción entre las moléculas del gas se pueden despreciar.
El volumen ocupado por las moléculas de gas es insignificante en comparación con el volumen del recipiente que lo contiene.
El movimiento de las moléculas de gas es aleatorio y continuo.

Un modelo de los gases reales: el gas ideal

Para estudiar los gases reales se utilizó un modelo idealizado llamado el modelado de gas ideal, que modela bien un gas real de dificil licuefacción, en bajo presión y alta temperatura. Para el estudio de los gases es muy importante lo siguiente:

La ley de Avogadro: Que dice que volúmenes iguales de gases bajo las mismas condiciones de temperatura y presión, tienen el mismo número de moléculas. Como el número de moléculas de un gas es un número muy grande, nos referimos al número de moléculas como un múltiplo de un número muy grande llamado mol. Así como una decena contiene 10 unidades y una docena contiene 12 unidades, basta pensar en el mol como "una docena un más grande."
1 mol de cualquier gas: La temperatura de 0 ° C y 1 atm de presión ocupa el volumen de 22.4 litros y contiene $6,023 \times 10^{23}$ moléculas.

Número de Avogadro $(N_0)$: Es el número $$N_0 = 6,023 \times 10^{23},$$ que facilita la comunicación y la escrita del número de moléculas en un gas. Es mucho más fácil decir que en un cilindro de gas hay 1 mol de decir que hay 602.300.000.000.000.000.000.000 moléculas.
C.N.T.P. - Condiciones Normales de Temperatura y Presión: Se refiere a una temperatura de 0 ° C y 1 atm.

Ecuación de estado de un gas ideal

Cada estado de equilibrio de un gas se caracteriza, desde el punto de vista macroscópico, por las siguientes propiedades macroscópicas:

presión $(P)$ ,
volumen $(V)$ ,
temperatura $(T)$ .

En un gas ideal, las variables anteriores están relacionadas por la ecuación de estado: $$PV = n RT,$$ donde $n$ es el número de moles del gas y $R$ es la constante universal de los gases perfectos y vale $$R = 0.082 ~ atm \cdot l/mol \cdot K \\ = 8.31 ~J/mol \cdot K.$$

Es estremamente importante observar que esta ecuación no tolera otras escalas de temperatura, sólo temperaturas en Kelvin pueden ser utilizados. Si tenemos medidas en grados Celsius o Fahrenheit, debemos transformarlas en Kelvin primero.

Ley general de los gases perfectos o ideales

La ley del gas ideal nos ayuda a calcular lo que va a pasar después de un transformación efectuada en el gas, véase el gráfico a continuación.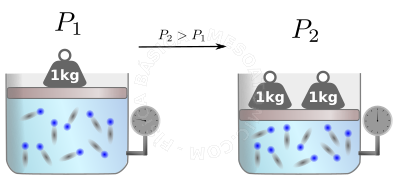

**Transformación en un gas perfecto.** Considere un gas dentro de un recipiente e inicialmente a una presión $P_1$, ejercida por el peso de una masa de $1kg$, ocupando un volumen $V_1$ y a una temperatura $T_1$. Si añadimos más masa, aumentando la presión a un valor $P_2$, este gas ocupará un nuevo volumen $V_2$ y también tendrá una nueva temperatura $T_2$. En el caso de un gas perfecto (ideal) la relación entre estas cantidades será determinado por la Ley General de gas ideal.

Sabemos que para un gas ideal podemos usar la fórmula $PV = n RT$, pero si el gas está confinado dentro de un contenedor, que siempre tendrá el mismo número de moles de modo que: $$\frac{PV}{T} = nR = \text{Constante}.$$ Luego, como el número de moles es el mismo para estado $1$, antes de la transformación, y para estado $2$, después de la transformación, se tiene que $$\frac{P_1.V_1}{T_1} = \frac{P_2.V_2}{T_2} = C^{te},$$ donde $P_1, V_1$ y $T_1$ son las variables de estado inicial antes de la transformación, y $P_2, V_2$ y $T_2$ son las variables después de la transformación. Recuerde que $T_1$ y $T_2$ es la temperatura en grados Kelvin.

Transformaciones de los gases

Los gases sufren cambios de estado cuando se producen trabajo en una máquina, es decir, pasan de un estado inicial a un estado final. Estas transformaciones pueden ocurrir de varias maneras, algunas de ellas son:

Transformación isobárica: Se produce a presión constante, entonces, $P_1 = P_2 \Rightarrow \frac{V_1}{T_1} = \frac{V_2}{T_2}$ ;
Transformación isotérmica: Se produce a temperatura constante, entonces $T_1 = T_2 \Rightarrow P_1.V_1 = P_2.V_2$
Transformación isocórica (isovolumétrica): Se produce a volumen constante, entonces $V_1 = V_2 \Rightarrow \frac{P_1}{T_1} = \frac{P_2}{T_2}$
Transformación adiabática: Se produce sin intercambio de calor entre el gas y el medio, entonces $Q_1 = Q_2$

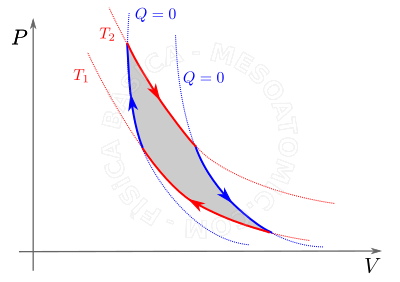
La figura a continuación ilustra algunas de estas transformaciones.

**Diagrama $P \times V$ .** La figura ilustra las transformaciones isotérmicas (líneas rojas) y adiabática (líneas azules). Estos dos cambios son muy importantes en el estudio de las máquinas térmicas.

El trabajo en las transformaciones de los gases

A diferencia de lo que se considera en la mecánica, el trabajo de un gas depende del estado inicial, final y de los intermedios también. El trabajo realizado por los gases en diferentes transformaciones o procesos se describen a continuación.

Proceso isobárico ( $P = C^{te}$ )

El trabajo $W$ realizado por una masa gaseosa en un proceso isobárico ( $P = \text{Constante}$ ), que tuvo un cambio de volumen $\Delta V = \text{volume final} - \text{volume inicial}$ es $$W = P \cdot \Delta V.$$

Cualquier transformación

El trabajo realizado en una masa de gas durante cualquier transformación es numéricamente igual al área bajo la curva en el gráfico de $P \times V$ (ver tabla a continuación). Para diferentes transformaciones tendremos diferentes signos para el trabajo, de modo que:

A: Expansión $V_f\gtV_i \Rightarrow \Delta V\gt0 \Rightarrow W\gt0 $ ,

B: Compresión $V_f \lt V_i \Rightarrow \Delta V\lt0 \Rightarrow W\lt0 $ ,

C: Volumen constante $V_f=V_i \Rightarrow \Delta V = 0 \Rightarrow W=0 $ ,

donde un trabajo positivo puede ser interpretado como el trabajo realizado por el gas y el trabajo negativo realizado sobre el gas.

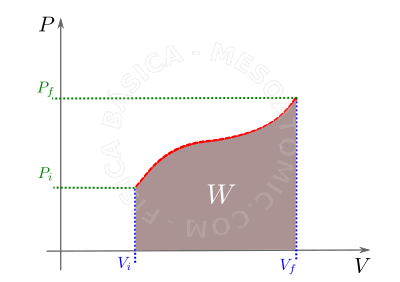
**El trabajo realizado por un gas.** Para un gas que sufre una transformación tal que su presión y volumen varían con una función dada (línea roja), el trabajo está dada por el área bajo la curva (área de color marrón).

Transformación ciclica

Es la transformación en la cual, después de su paso, las condiciones finales de presión, volumen y temperatura son iguales a las iniciales, y el área limitada por el bucle en el diagrama de $P \times V$ mide el trabajo realizado sobre el mismo, véase la figura a continuación.

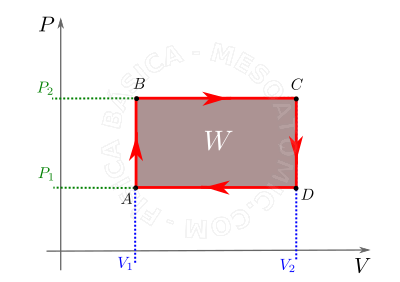
**Transformación cíclica.** Para una transformación cíclica, como se ilustra con las líneas rojas, el trabajo realizado es el área dentro del bucle, el área de color marrón.

Por convención, el trabajo realizado en el ciclo es positivo si se recorre en sentido horario, y negativo si es recorrido en sentido anti-horario.

En nuestro APP usted encuentra: Contenido accesible sin conexión Visualizador de Progreso Cientos de ejemplos Calculadora y Convertidor de unidades ¡Es mucho más!