- Termofísica
- /
- Temperatura
- /
- Dilatación de sólidos
La dilatación térmica es el fenómeno donde los cambios de volumen de un cuerpo es causado por la variación de su temperatura, por lo general se produce debido al aumento en el grado de agitación de sus moléculas y por lo tanto hay un aumento en la distancia media entre ellos.
La dilatación de sólidos isotrópicos
- Dilatación o expansión volumétrica
- Objetos en los cuales las tres dimensiones son del mismo orden de grandeza, a menudo varían significativamente en tres dimensiones, es decir, no se puede descuidar ninguna variación. Algunos ejemplos son: cubos, adoquines, etc. Para esta clase de objetos debe implementarse la expansión volumétrica, cuya fórmula es $$\Delta V = V_0 \gamma \Delta T,$$ donde \( \Delta V = V - V_0\) es la variación del volumen, \(\gamma\) es el coeficiente de expansión térmica volumétrica y \(\Delta T = T - T_0\) variación de la temperatura.
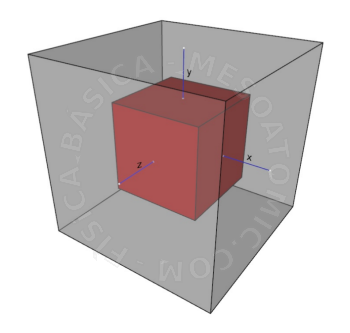
Ilustración de la expansión volumétrica. Considere el bloque rojo en la figura, al calentar el bloque este se irá dilatando y ocupará un nuevo volumen (bloque gris transparente). En este caso, el nuevo volumen, considerando sus dimensiones duplicaron su tamaño, será \(V = 2x \cdot 2y \cdot 2z\) y por lo tanto la variación de volumen será \(\Delta V = 2x \cdot 2y \cdot 2z - x \cdot y \cdot z = 7x \cdot y \cdot z \). - Dilatación superficial
- Algunos objetos tienen un área de superficie muy grande en relación con su volumen, por ejemplo: hojas, placas, baldosas, etc. Para esta clase de objetos la variación de su espesura es generalmente despreciable en comparación con la superficie, de modo que la variación del área \(\Delta A\) de superficie viene dada por: $$\Delta A = A_0 \beta \Delta T,$$ donde \(A_0\) es el área inicial, \(\beta\) es el coeficiente de expansión superficial y \(\Delta T\) es la variación de la temperatura que el sistema ha experimentado.
- Expansión lineal
- A veces sólo una de las dimensiones de un objeto tiene de interés práctico. Cuando este es el caso, sólo se estudia la variación de la longitud de interés, y no nos preocupamos por las otras dos dimensiones del objeto. Un ejemplo práctico es la dilatación sufrida por un carril de una vía férrea. Aunque la altura y el espesor del carril varía, la variación de su longitud es la que normalmente es de interés, de lo contrario si no se tiene en cuenta la expansión térmica durante la construcción de la vía férrea, este puede terminar deformandose. En el caso de expansión lineal la fórmula es $$\Delta L = L_0 \alpha \Delta T,$$ donde \(\Delta L = L - L_0\) es la variación en la longitud sufrido después de un cambio de temperatura \(\Delta T = T - T_0\) , \(\alpha\) es el coeficiente de expansión térmica lineal y \(L_0\) es la longitud del sistema antes de que sufra una variación en la temperatura.
- Relación entre los coeficientes de expansión para materiales isótropos:
- $$\beta \approx 2 \alpha$$ $$\gamma \approx 3 \alpha$$ $$\beta \approx 2/3 \gamma$$
Coeficiente de dilatación lineal Material Valor ( \(10^{-6} K^1\) ) Hielo \(51\) Cobre \(17\) Acero \(11\) Vidrio (común) \(9\) Vidrio (Pyrex) \(1,2\) Invar (hierro + níquel) \(0,7\) Cuarzo fundido \(0,5\) Comentarios
Desde el punto de vista de la expansión, los sólidos se consideran isotrópicos cuando las expansiones en diferentes direcciones son proporcionalmente iguales. Esto no ocurre para algunos cristales, que se llaman anisotrópicos, que dilatan proporcionalmente más en una dirección que en otras.
Los materiales con coeficientes bajos de expansión se dilaten bajo la misma variación de la temperatura.
En general, el coeficiente de dilatación varía con la temperatura, pero en muchos casos prácticos, se puede prescindir de esta variación. Este enfoque es válido cuando estamos interesados en un rango de temperatura que no es demasiado grande y no cuando el material se acerca a su punto de fusión.
