- Óptica
- /
- Reflejos y Espejos
- /
- Espejo plano
"El espejo testa la reflexión de la luz y la irreflexión de los hombres"
Gar-Mar
El espejo plano
Es un sistema óptico estigmático, porque combina siempre un punto objeto con un punto imagen. El también combina, de un objeto real, siempre imagen virtual, derecha, y el mismo tamaño del objeto, y hay una inversión de la imagen en relación con el eje paralelo al espejo, pero no hay inversión de arriba a abajo (ver figura abajo). Llamamos a este tipo de imagen de especular o enantiomorfa. 
- Campo visual
- Es la región del espacio que se puede observar a través del espejo.

Ilustración del campo visual (área gris) de un observador en un espejo plano. - Translación de espejo
- Cuando un espejo plano se mueve paralelamente a su posición inicial, la imagen de un objeto fijo se sufre un desplazamiento que es dos veces el desplazamiento de espejo en la misma dirección.
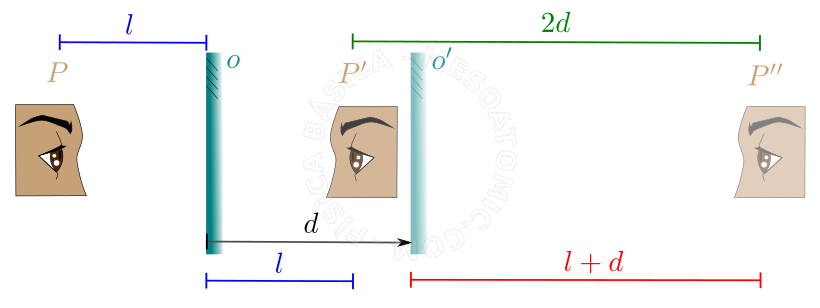
Desplazamiento de un espejo plano. Para un objeto en el punto \(P\) y un espejo en la posición \(o\), una imagen en el punto \(P'\) es generada. Si el espejo es transladado de la posición \(o\) a \(o'\), la imagen se moverá desde el punto \(P'\) hasta el punto \(P''\). Como el espejo fue transladado de una distancia \(d\), la imagen será transladada una distancia \(2d\). - Rotación del espejo
- Si un espejo plano sufre una rotación de un ángulo \(\alpha\) en torno de un vertice del espejo, el rayo reflejado experimenta un giro \(2 \alpha\). Este resultado se deduce usando las leyes de la reflexión y de la geometría plana (ver figura abajo).
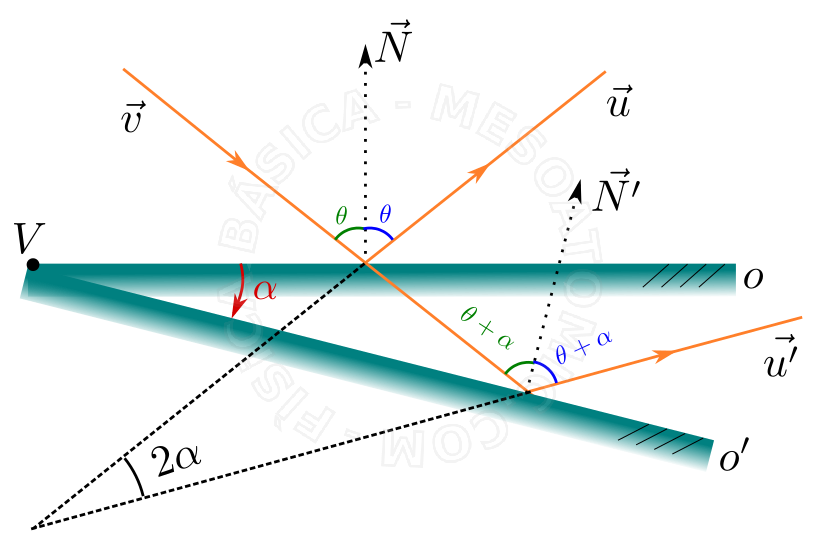
La rotación de un espejo plano. Considere un rayo incidente \(\vec{v}\) en un espejo plano \(o\) que ha reflejado haz \(\vec{u}\) . Si rotacionarmos el espejo en un ángulo \(\alpha\) en relación con el vértice \(V\) a la posición \(o'\) , el haz transmitido \(\vec{u}\) se hace girar para \(2 \alpha\) , suponiendo que la dirección \(\vec{u'}\) . - Asociación de espejos planos
- Si asociamos dos espejos planos, de modo que tengan un ángulo \(\alpha\) entre ellos, tendremos \(n\) imágenes para un objeto \(P\) situado entre los espejos, de tal manera que: \begin{equation} n=\frac{360}{\alpha}-1, \end{equation} donde \( 0^o \lt \alpha \lt 180^o\), y la expresión sólo es válida para valores de \(\alpha\) que sean divisores de \(360\), por ejemplo, \(120^{o}\) , \(90^{o}\) , \(72^{o}\), etc. Cuando \(\frac{360}{\alpha}\) es un número entero impar, la expresión sólo es válida para un objeto situado en la bisectriz del ángulo \(\alpha\) .
-

Asociación de dos espejos con un ángulo recto entre ellos ( \(\alpha = 90^o\) ). En este caso tenemos \(n = \frac{360}{90} - 1 = 3\) imágenes.
