- Óptica
- /
- Reflejos y Espejos
- /
- Espejo esférico
Un espejo esférico es un casquete esférico donde se produce reflexión regular de la luz.
Espejos esféricos
Tipos de espejos:
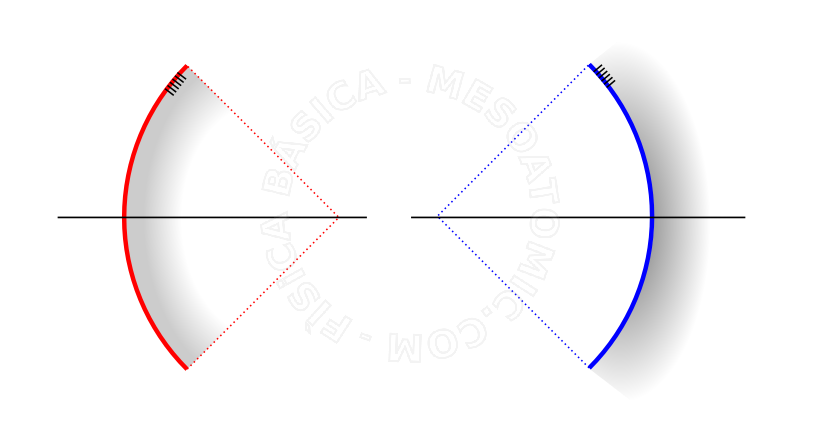
- Espejo esférico cóncavo
- Cuando la superficie reflectante esta del lado interno de la tapa esférica.
- Espejo esférico convexo
- Cuando la superficie reflectante esta del lado exterior de la tapa esférica.
Elementos geométricos

- Centro de curvatura \((C)\)
- Es el centro de la esfera que contiene el casquete esférico;
- Radio de curvatura \((r)\)
- Es el radio de curvatura que contiene el casquete esférico;
- Vértice del espejo \((V)\)
- Es el punto medio de la calota esférica;
- Eje principal \((u)\)
- Es la línea recta que contiene el centro \(C\) y el vértice \(V\) del espejo;
- Eje secundario \((u')\)
- Es cualquier línea que contiene el centro de \(C\) , pero que no contiene el vértice \(V\) del espejo;
- Foco principal \((F)\)
- Es el punto entre el centro de curvatura y el vértice del espejo, para los espejos esféricos de Gauss. La ecuación del foco es \(f=\frac{r}{2}\) ;
- Enfoque secundario \((F_s)\)
- Es el punto focal que pertenece a un eje secundario y no al eje principal. Cuando un haz de rayos paralelos incidente sobre un espejo esférico paralelamente a uno de sus ejes secundarios, se produce un haz convergente, en el caso del espejo cóncavo, y divergente en el caso convexo. El vértice \(F_s\) de origen del pincel de luz de estos rayos refletidos se situan en ese eje secundario e constituye uno de los focos secundarios.
Propiedades da reflexión de los rayos de luz
Suponiendo que las trayectorias de los rayos de luz forman ángulos pequeños con el eje óptico (aproximación paraxial), para un espejo esférico tenemos las siguientes reglas para de reflexión:
- Un rayo incidente de paralelamente al eje principal se refleja en relación al foco principal.
- Un rayo incidente en relación al foco principal se refleja paralelamente al eje principal.
- Un rayo incidente en la dirección de un eje del espejo se refleja sobre sí mismo.
- Un rayo incidente en el vértice espejo, y oblicuo a un eje, se refleja simétricamente con respecto a este eje.
- Todo rayo de luz que incide sobre un espejo esférico oblicuamente al eje principal, al reflejarse, pasa a través de su foco secundario.
Imagen producida por un espejo convexo
Suponiendo que las trayectorias de los rayos de luz de un objeto forman ángulos pequeños con el eje óptico (aproximación paraxial), en esta situación la imagen de un espejo convexo es siempre: virtual, derecho y menor.
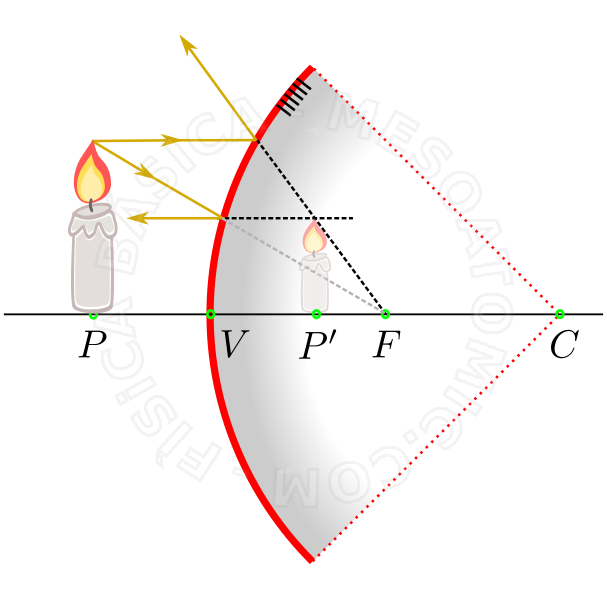
Imagen producida por un espejo cóncavo
Suponiendo que las trayectorias de los rayos de luz de un objeto forman pequeños ángulos con el eje óptico (aproximación paraxial), es posible encontrar las diferentes imágenes que un espejo cóncavo puede producir en esta situación (ver figura).
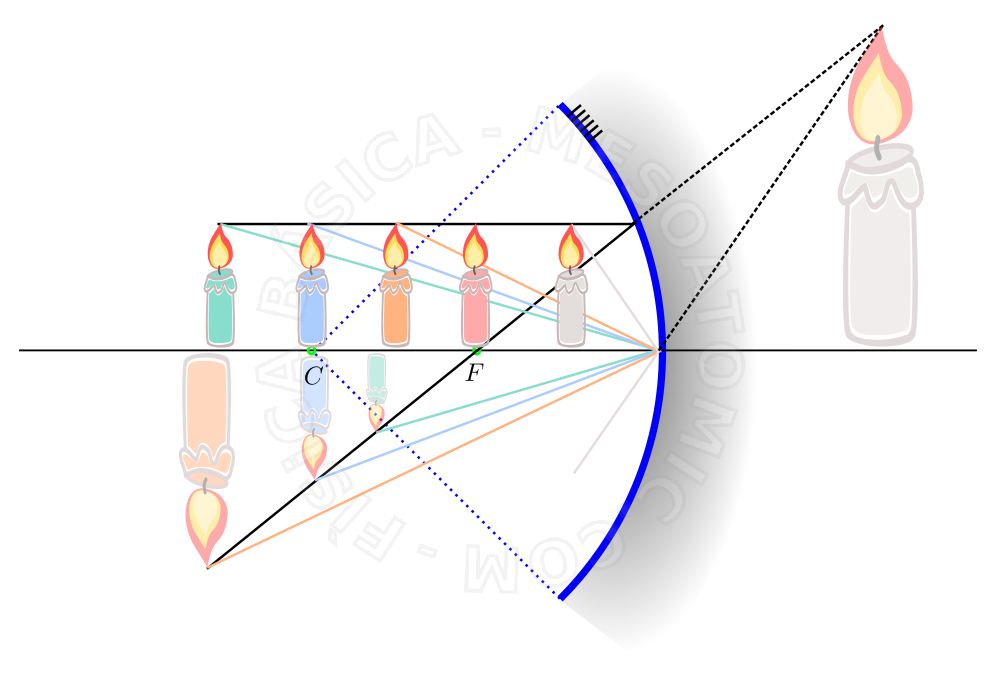
- Vela verde
- Es un objeto más allá del centro de curvatura, cuya imagen es real, invertida y más pequeña.
- Vela azul
- Es un objeto sobre el centro de curvatura, cuya imagen es real, invertida y del mismo tamaño.
- Vela naranja
- Es un objeto entre el centro de curvatura y el foco, cuya imagen es real, invertida y más grande.
- Vela roja
- Es un objeto en el plano focal, cuya imagen es impropia (se forma en el infinito).
- Vela de color gris
- Es un objeto entre el foco y el vértice, cuya imagen es virtual, derecha y más grande.
Referencial de Gauss
Para realizar el estudio analítico/algebraico de los espejos esféricos, utilizamos la referencia de Gauss donde
- El eje de las abcisas
- Coincide con el eje principal del espejo, con origen en el vértice y orientado en el sentido contrario al de la luz incidente;
- El eje de las ordenadas
- Es perpendicular al eje principal, con origen en el vértice del espejo. El eje de las ordenadas está orientado para que la ordenada \(o\) del objeto sea positiva.
-
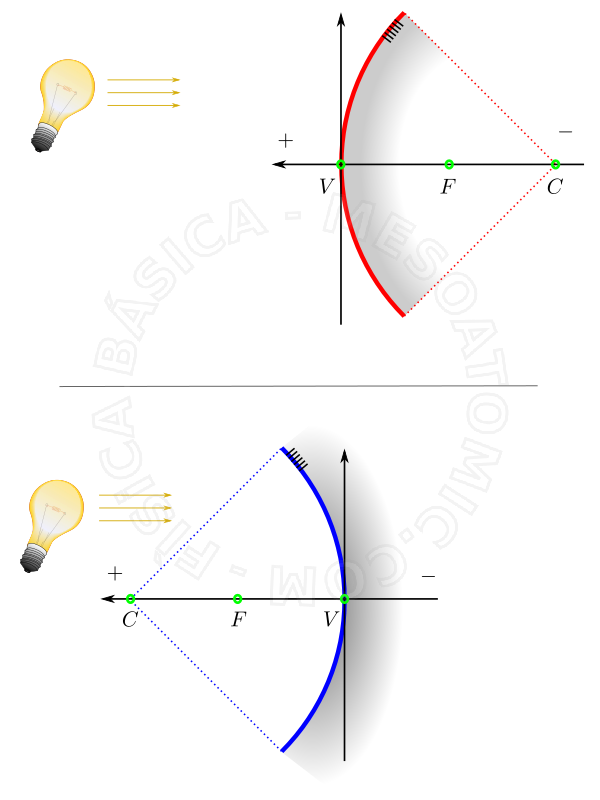
Ilustración del referencial de gauss para el espejo convexo (rojo) y cóncavo (azul).
Ecuación del aumento lineal transversal:
La amplificación \(A\), o aumento lineal de una imagen en un espejo esférico está dada por \begin{equation} A=\frac{i}{o}=\frac{-p'}{p}\ \end{equation} donde \(p\) es la distancia del objeto al vertice del espejo, \(p'\) la distancia de la imagen al vertice del espejo, \(o\) el tamaño del objeto, \(i\) tamaño de la imagen. Tenga en cuenta: para una imagen derecha, tenemos que \(A\gt0\) y para una imagen invertida, tenemos \(A\lt0\) .
Ecuación Gauss (puntos conjugados).
La imagen de un objeto, colocada a una distancia \(p\) de un espejo de distancia focal \(f\), se forma a una distancia \(p'\) del espejo, de tal manera que \begin{equation} \frac{1}{f}=\frac{1}{p}+\frac{1}{p'}, \end{equation} donde \(p\) es positiva para objetos reales y negativa para objetos virtuales, \(f\) es positiva para el espejo cóncavo y negativo para el convexo, y \(p'\) es positivo para una imagen real y negativa para una imagen virtual. Esta ecuación también es válida sólo para la aproximación paraxial, es decir, para los rayos de luz que forman pequeños ángulos con el eje principal del espejo.
Observaciones
- Las cantidades \(f\) , \(p\) , \(p'\) , \(i\) , \(o\) y \(A\) son algebraicas, es decir, que deben ser introducidos en las ecuaciones con sus signos (positivo o negativo) a la que puede producir resultados correctos.
- A veces los sistemas ópticos utilizan dos (o más) espejos, y la imagen formada por el primer espejo sirve como objeto para el segundo espejo. En algunas situaciones, tal objeto se encuentra detrás del segundo espejo. En este caso, la distancia del objeto es negativo, y se dice que el objeto es virtual.
