- Ondulatorio
- /
- Mov. Armónico Simple
- /
- MAS y péndulo simple
El oscilador armónico simple es un sistema aislado de fuerzas externas, además de no tener ningún amortecimiento. El también se conoce como sistema de masa-resorte. En este sistema, la única fuerza que actúa es del resorte elástico.
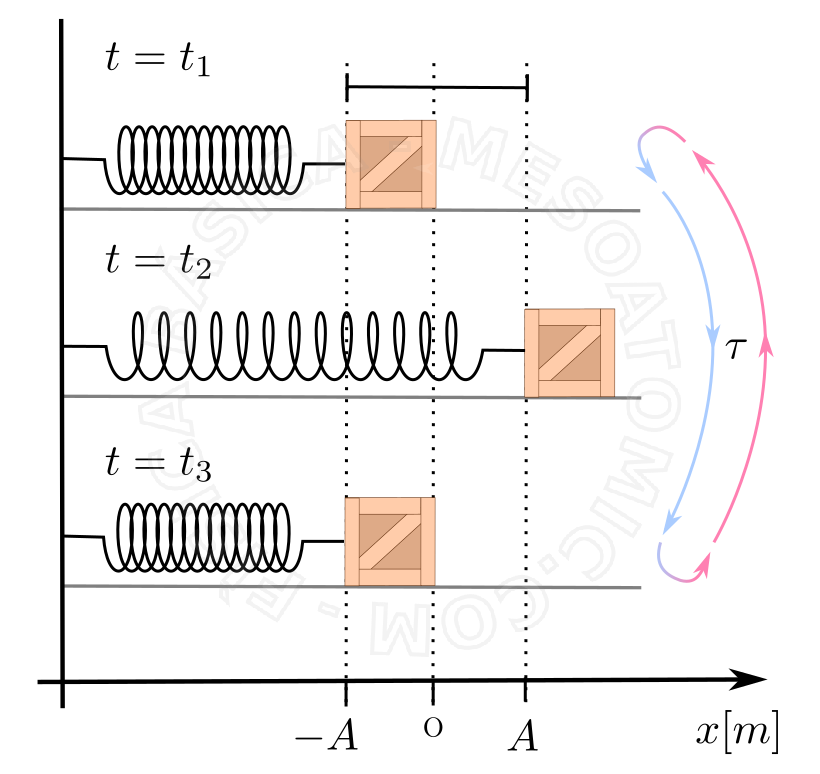
Oscilador armónico simple
Tenemos para este sistema para las siguientes características:
- 1. El cuerpo unido al resorte realiza un movimiento armónico simple (MAS)
- 2. La elongación en el MAS es, en módulo, la misma deformación (distensión o contracción) del resorte.
- 3. La fuerza resultante sobre el cuerpo es la misma fuerza elástica aplicada por el resorte cuando la fuerza de peso y la normal son perpendiculares al movimiento, y la fricción es insignificante.
- 4. En el equilibrio, la fuerza elástica (fuerza resultante) es cero, y el resorte no se deforma.
Energia
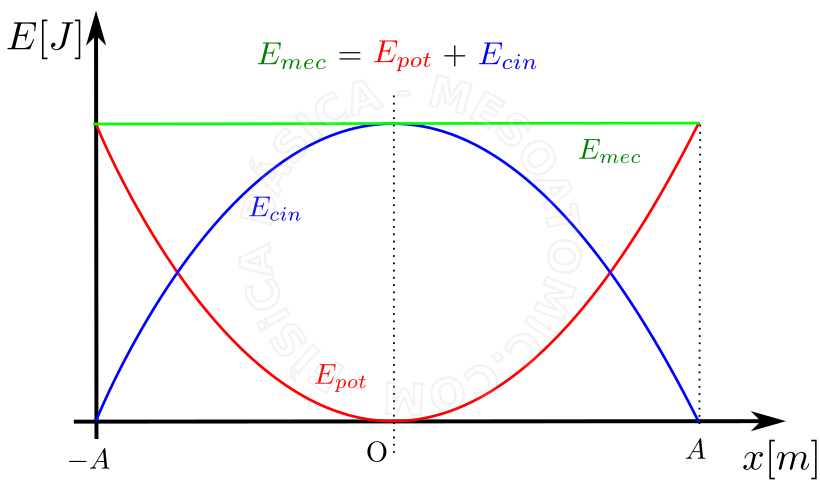
Dado un sistema masa-resorte u otro oscilador armónico simple, donde las fuerzas de fricción son despreciadas, habrá conservación de la energía mecánica, es decir, para cualquier configuración del sistema la suma de la energía cinética más la potencial es constante. En el caso del sistema masa-resorte, tenemos:
- \( E_c = m \frac{v^2}{2} \)
- \( E_{el} = \frac{kx^2}{2} \)
- \( E_{mec} = E_c + E_{el} = \frac{k A^2}{2} \)
- \( E_{el} = \frac{kx^2}{2} \)
Asociación de resortes
Imaginemos que tenemos dos cuerpos A y B, y queremos tener más de un resorte entre ellos. Llamamos de "Asociación de serie" cuando unimos los resortes uno tras del otro, en una fila. Ya en paralelo, cada resorte está conectado entre A y B.
En el cálculo, podemos sustituir todas las constantes elásticas para un equivalente, dependiendo de la configuración:
- Serie
- \( \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} \)
- Paralela
- \( k_{eq} = k_1 + k_2 \)
El péndulo simple
Es un dispositivo que consta de una partícula de masa \(m\) suspendido por un cuerda (vara o alambre) masa despreciable y longitud \(L\) . En los relojes antiguos (relojes de caja alta) los péndulos simples se utilizan para marcar el paso del tiempo. El péndulo se comporta como un oscilador armónico cuando la amplitud de la vibración del mismo es pequeña en relación a la vertical (ángulos pequeños).
Periodo de un péndulo simple
Teniendo en cuenta que la fricción es despreciable, usando las leyes de Newton es posible deducir el período del péndulo simple para ángulos pequeños, es decir: $$ \tau = 2 \pi \sqrt{\frac{L}{g}},$$ donde \(g\) es la aceleración de la gravedad y \(L\) es la longitud del péndulo. Este es período tiene las siguientes propiedades:- Sólo depende de la longitud de la cuerda y la aceleración local de la gravedad
- No depende de la masa del péndulo
- Es isócrona, es decir, el período no depende de la amplitud.

