MAS: Conceptos Básicos

Ondulatorio
/
Mov. Armónico Simple
/
MAS: Conceptos Básicos

En la naturaleza encontramos con frecuencia fenómenos que se repiten continuamente. Las estaciones, las fases de la luna y los latidos del corazón, son ejemplos de estos fenómenos. El movimiento armónico simple (MAS) es un modelo utilizado para describir diversos fenómenos de este tipo, todo movimiento armónico simple es periódico y oscilatorio.

Conceptos básicos

Podemos presentar dos definiciones para MAS:

Def. 1: El movimiento se realiza por una partícula sometida a una fuerza proporcional al desplazamiento y de signo opuesto. La fuerza del MAS es del tipo: $ F \propto x $ , y $x$ , el desplazamiento desde la posición de equilibrio. Notación: El símbolo " $\propto$ " se refiere a la proporcionalidad.
Def. 2: Se llama MAS a cualquier movimiento que sigue una ley representada por una función sinusoidal (o cosenoidal) del tipo: $$ x = A sen(\omega t + \theta_0)$$ o $$ x = A cos(\omega t + \theta_0)$$

Otras definiciones importantes son:

Movimiento periódico: Es todo movimiento donde se repite la misma situación en intervalos de tiempo iguales.
Movimiento oscilatorio (vibración): Todo movimiento simétrico alrededor de un punto de equilibrio.

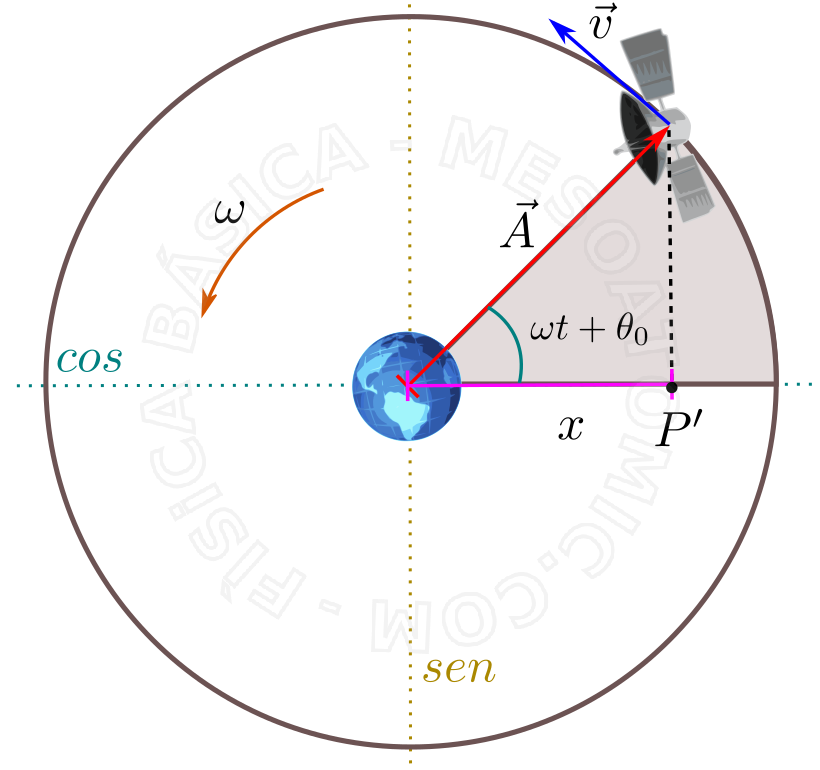
**Ilustración del MAS.** El satélite se mueve realizando un movimiento circular uniforme (MCU) puede ser visto como un MAS si tenemos en cuenta sólo la componente $x$ (o $y$ ) del vector de posición $\vec{A}$. El vector $\vec{A}$ gira en sentido antihorario alrededor del origen (en este caso la tierra) con velocidad angular $\omega$ y forma un ángulo $ \omega t + \theta_0 $ con el eje x.

Funciones dependientes del tiempo del MAS:

Para escribir la función de tiempo del MAS se necesita saber:

Amplitud ( $A$ ): del MAS es la medida del desplazamiento del origen del sistema hasta el punto máximo.
Fase inicial ( $\theta_0$ ):: Es el desvío del cuerpo de la posición de equilibrio en el tiempo inicial, $t = 0$ .
La velocidad angular ( $\omega$ ):: Es la "pulsación" o la frecuencia angular del movimiento. Que es dada por $$ \omega = \frac{2 \pi}{\tau} = 2 \pi f,$$ donde $\tau$ es el período y $f$ es la frecuencia de movimiento.

Con esto, tenemos que:

Elongación ( $x$ ): es la distancia del sistema al punto de equilibrio, y se da por $$x = A cos ( \omega t + \theta_0 ).$$
Velocidad ( $v$ ): $v = -\omega A sen ( \omega t + \theta_0 )$
Aceleración ( $a$ ): $a = -\omega^2 A cos ( \omega t + \theta_0 )$

Velocidad de elongación en función del tiempo:: $v = \omega^2 (A^2- x^2) $
Velocidad en los puntos de inversión:: $v = 0 $
La velocidad en el punto central:: $v = \pm \omega^2 x $ (Max y Min)
Aceleración en función de la elongación:: $a = -\omega^2 x $
Aceleración en función de la elongación:: $a = \pm \omega^2 A $ (max y min).
La aceleración en el punto medio:: $a = 0 $

En nuestro APP usted encuentra: Contenido accesible sin conexión Visualizador de Progreso Cientos de ejemplos Calculadora y Convertidor de unidades ¡Es mucho más!

Conceptos básicos

Funciones dependientes del tiempo del MAS:

ESTUDIO FÍSICO A CUALQUIER HORA EN CUALQUIER LUGAR