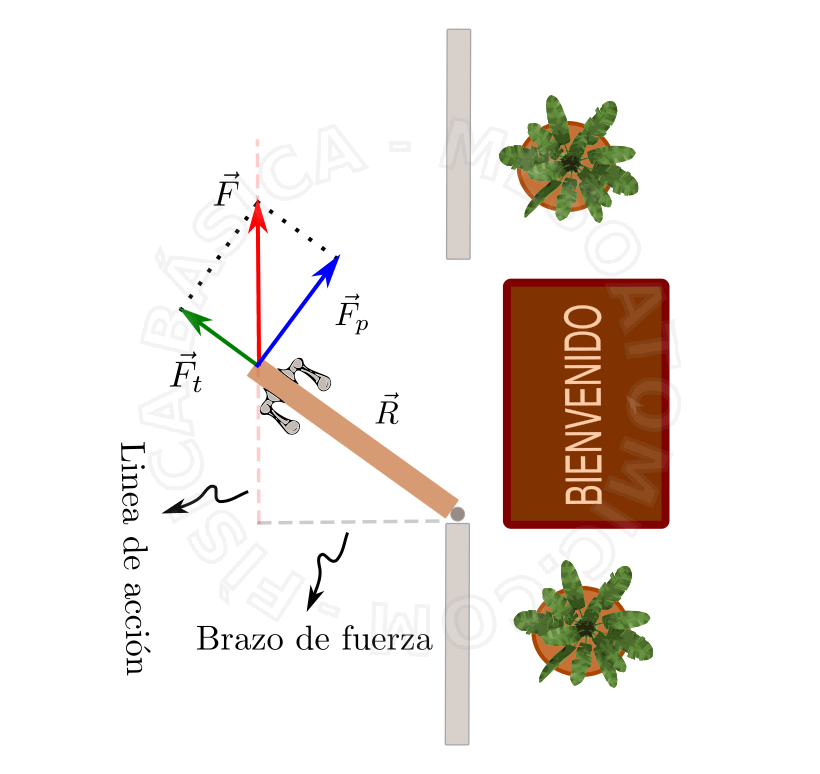
La figura anterior muestra una fuerza que actúa sobre una puerta. Dependiendo de cómo es aplicado, puede hacer que la puerta gire más fácilmente. Para el análisis de este tipo de problemas, las siguientes grandezas son importantes:

Brazo de palanca de fuerza o de momento \((b)\)

Dado un eje de rotación, el brazo de una fuerza \(b\) es la distancia más corta entre el eje de rotación y la línea de fuerza de la acción.

Momento de una fuerza \((M)\)

El valor algebraico del momento de una fuerza, o par, está dada por la expresión: $$M = \pm F d,$$ donde \(F\) es la magnitud de la fuerza aplicada al cuerpo y \(d\) es el brazo de la fuerza sobre el eje dado.

Se adopta la siguiente convención de signos: Cuando \(F\) tiende a girar el cuerpo en el sentido anti-horario tiene un signo positivo \((+)\) y cuando \(F\) tiende a girar el cuerpo en el sentido horario tiene signo negativo \((-)\) ,

Momento de una fuerza con respecto a un eje \(o\)

Es posible definir el momento de un vector de fuerza a través de la siguiente ecuación: $$ \vec{M}_o = \vec{R} \times \vec{F},$$ donde \(\times\) es el producto vectorial entre fuerza \(\vec{F}\) y el vector de posición de la fuerza, \(\vec{R}\) en relación con el eje \(o\) . De manera equivalente, es posible para escribir un producto vectorial como $$ M = F sen(\theta) R,$$ donde \(\theta\) es el ángulo más pequeño entre \(\vec{F}\) y \(\vec{R}\). La figura superior ilustra estos vectores, donde el vector \(R\) es la dirección que coincide con el punto de origen y el eje de rotación del mismo.

Hay una convención para la dirección del vector \(\vec{M}\) como el producto vectorial deja claro, siempre es ortogonal al plano del sistema de rotación, y será positivo o negativo de acuerdo con la dirección de rotación, la convención como se mencionó anteriormente. Es decir, para una rotación en el sentido horario, el vector momento de la fuerza apunta dentro del plano de rotación, en el caso de un movimiento antihorario, el vector apunta fuera del plano de rotación.

Momento resultante

El momento de una fuerza con respecto a un eje del sistema es igual a la suma de los momentos de las fuerzas que constituyen el sistema en relación con el mismo eje, es decir $$ \vec{M}_r = \sum_i^n \vec{M}_i $$ Si el momento resultante de las fuerzas que actúan sobre un cuerpo rígido es cero, no tiene la aceleración angular, o el está girando con velocidad angular constante o no esta rotando. En forma matemática: $$ \vec{M}_r = \sum_i^n \vec{M}_i = \vec{0} $$ cuando no hay aceleración rotacional del cuerpo.

Binario

Binário es un sistema constituido de dos fuerzas de la misma magnitud y dirección, pero sentidos opuestos y diferentes líneas de acción, como se muestra en el Malabar en la figura de arriba, en donde \(|\vec{F}_1|=|\vec{F}_2|=F\) . Para este sistema se aplica lo siguiente:

• La fuerza resultante es un cero binario, entonces no hay translación del cuerpo.
• Un binário tiende a producir solamente una rotación en el cuerpo donde se aplica.
• Un binário puede ser equilibrado por otro binário opuesto.
• La suma de los momentos de fuerza es constante e independiente de cualquier centro de distribución.

El torque para el binário es \( M = 2F \frac{L}{2} = FL\) , donde \(L\) es la longitud del cuerpo. En este caso \(d=\frac{L}{2}\), ya que en ausencia de un eje fijo los cuerpos girar en relación a su centro de masa.