- Mecánica
- /
- Estática
- /
- Estática de sólidos
Hay dos formas sencillas de movimiento para un sistema rígido: traslación y rotación. Cualquier otra forma de movimiento posible, por más compleja que sea, siempre se puede considerar como la superposición de una rotación y una traslación.
Estática de los sólidos
No siempre es posible considerar el cuerpo como una partícula puntual, en general, cuando estamos interesados no sólo en el desplazamiento de un objeto, sino también en su rotación, la siguiente definición es importante:
- Cuerpo rígido o sólido
- El modelo adoptado para objetos extenso considera que el tamaño y la forma de estos prácticamente no se altera cuando se somete a fuerzas externas, a pesar que los enlaces moleculares reales no sean perfectamente rígidos. Puentes, aviones y muchos otros objetos pueden considerarse buenos ejemplos de cuerpos rígidos, estos se deforman poco, y por la acción de fuerzas muy fuertes, se quiebran.
Los dos posibles tipos de movimiento de un cuerpo rígido se pueden definir como:
- Translación
- Es el movimiento que cambia la posición de un objeto, es decir, todos los puntos del cuerpo se mueven una distancia fija en la misma dirección.
- Rotación
- En el movimiento de rotación todos los puntos del cuerpo se mueven en arcos circunferenciales cuyos centros están en el mismo eje, llamado eje de rotación.
Equilibrio de los sólidos
Para que un sólido se encuentre en equilibrio en un marco de referencia inercial, es necesario satisfacer dos condiciones: una relacionada con la translación y la otra relacionada al equilibrio de rotación, que se definidas como sigue:
- Equilibrio de translación
- La condición de equilibrio de translación de un cuerpo rígido es que el centro de masa se encuentre en reposo o en movimiento rectilíneo uniforme, es decir, la resultante de las fuerzas externas que actúan sobre el cuerpo es cero. En forma matemática: $$\vec{F}_r = \vec{0}$$ donde \(\vec{F}_r\) es la resultante de las fuerzas en el sistema.
- Equilibrio de rotación
- La condición de rotación de equilibrio estático es que el cuerpo no gira. Para que esto suceda en un cuerpo rígido bajo la acción de un sistema de fuerzas, es necesario que la suma de los momentos de todas las fuerzas alrededor de cualquier eje sea cero. En forma matemática: $$ \vec{M_r} = \vec{0},$$ donde \(\vec{M_r}\) es el torque resultante en el sistema.
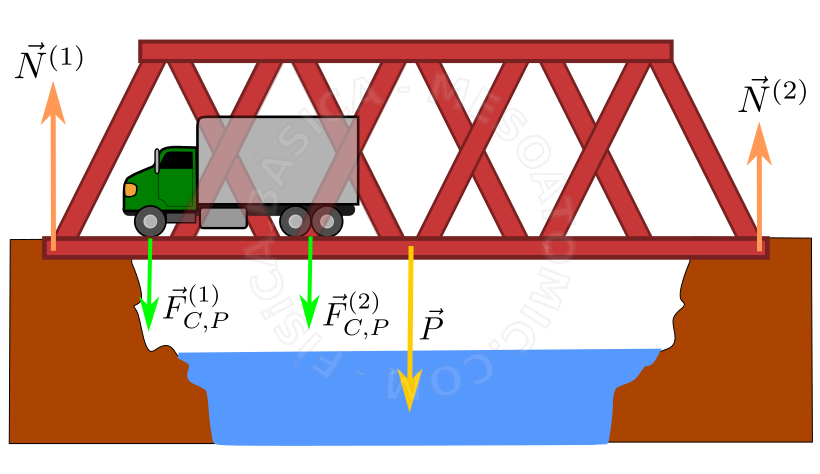
La figura superior ilustra un cuerpo extenso, el puente, que sufre la acción de diversas fuerzas. Considerando que el sistema de interés es el puente, para que se encuentre en equilibrio estático, las fuerzas que actúan en ella deben cumplir con las siguientes condiciones: que no haya translación, osea la resultante de las fuerzas debe ser cero, \begin{align} & +\vec{N}^{(1)} + \vec{N}^{(2)} + \vec{F}_{C,P}^{(1)} +\\ +& \vec{F}_{C,P}^{(2)} + \vec{P} = 0, \end{align} y para que no halla rotación, el torque sobre el puente también debe ser cero \begin{align} -& N^{(1)} d_{1} + N^{(2)} d_{2} + F_{C,P}^{(1)} d_{3} +\\ +& F_{C,P}^{(2)} d_{4}+ P d_{5}= 0, \end{align} en donde cada \(d_i\) es la distancia de cada fuerza con respecto al centro de masa del puente, vector de posición \(P\), por lo que \(d_5 = 0\) .
Teorema de Lamy
Si un sistema rígido está en equilibrio bajo la acción de las tres únicas fuerzas externas, \(F_1\) , \(F_2\) y \(F_3\) , no paralelas, el módulo de cada uno es proporcional al seno del ángulo entre los otros dos, a saber: $$ \frac{F_1}{sen(a)} = \frac{F_2}{sen(b)} = \frac{F_3}{sen(c)},$$ donde \(a\) , \(b\) y \(c\) son los ángulos entre las fuerzas, como se muestra en la figura siguiente. 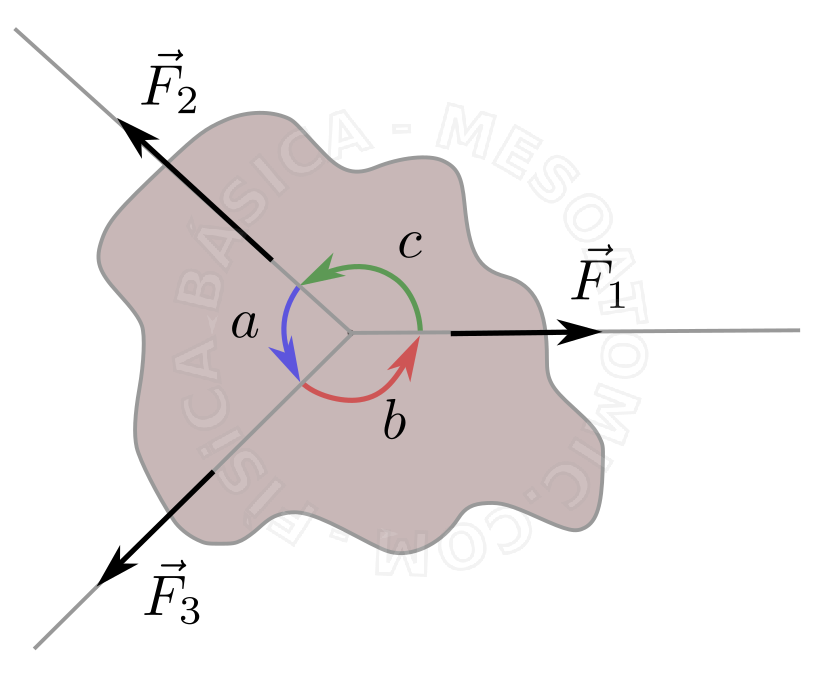
Teorema de Poisont
Cualquier sistema de fuerzas por más complejo que sea, siempre puede se reducido a una sola fuerza, conocida como la fuerza resultante, y a un binario, cuyo plano es ortogonal a la fuerza resultante.
