- Mecánica
- /
- Estática
- /
- Centro de masa
Centro de masa es el punto de un sistema de partículas que se mueve como si toda la masa y las fuerzas externas estuviesen concentradas en él.
Centro de masa
La determinación del centro de masa se calcula a través promedio ponderado: \begin{array} \\ X_{cm} &=\frac{m_1 x_1+m_2 x_2 +...+ m_n x_n}{m_1+m_2+...+m_n},\\ Y_{cm} &=\frac{m_1 y_1+m_2 y_2 +...+ m_n y_n}{m_1+m_2+...+m_n}, \end{array} donde el factor ponderante es la masa \(m_i\) de la \(i\)-ésima partícula y \((x_i,y_i)\) es su posición como se muestra en la siguiente figura. 
- El centro de masa de un sistema aislado, es decir, donde la resultante de las fuerzas es cero, se mueve en un movimiento rectilíneo uniforme, MRU, en cualquier referencia inercial.
- El centro de masa de un sistema de partículas se mueve como si fuera una partícula única sujeta a las mismas fuerzas como un todo. En este caso, se considera que la masa total del sistema se concentra en esta sola partícula.
- La cantidad de movimiento total de un sistema es igual al producto de la masa total por la velocidad del centro de masa.
- El centro de masa de un sistema que tiene una distribución de masa uniforme es el centro geométrico real (centroide).
Distribuición continua
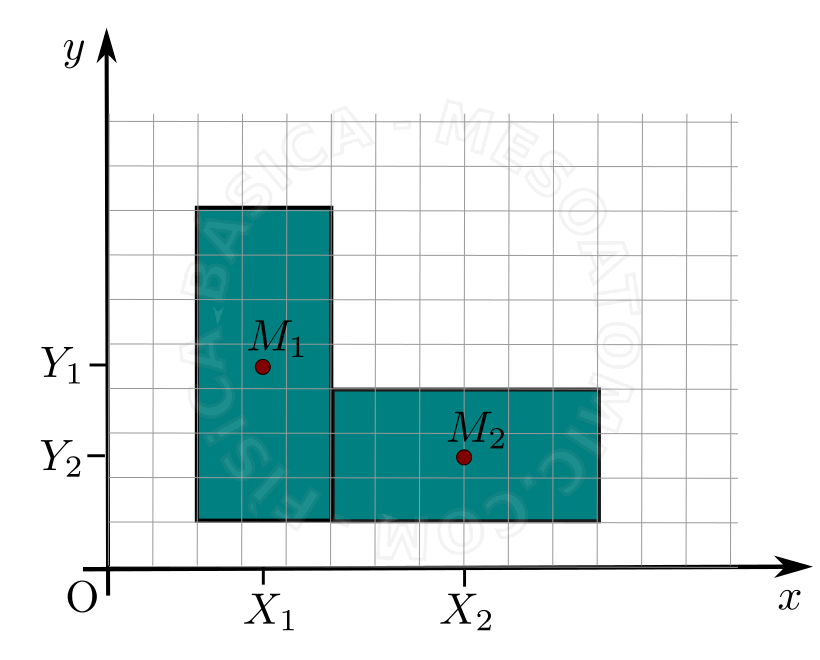
Para el caso de un cuerpo continuo como se muestra en la figura anterior, es posible simplificar el cálculo teniendo en cuenta que el cuerpo se compone de dos rectángulos donde la distribución de la masa sea homogénea. En este caso, el centro de masa de cada rectángulo es en su respectivo centroide y el centro de masa del sistema en su conjunto, los dos rectángulos, se puede calcular con las fórmulas: \begin{align} X_{CM} &= \frac{X_1 M_1 + X_2 M_2}{M_1 + M_2},\\ Y_{CM} &= \frac{Y_1 M_1 + Y_2 M_2}{M_1 + M_2}, \end{align} en donde \((X_i, Y_i)\) es la posición del centro de masa de la masa total del objeto \(M_i\) .
