- Mecánica
- /
- Dinámica
- /
- Trabajo y potencia
El trabajo es un proceso por el cual la energía puede transformarse de una forma a otra o transferirse de un objeto a otro, debido a la acción de una fuerza.
Trabajo de una fuerza
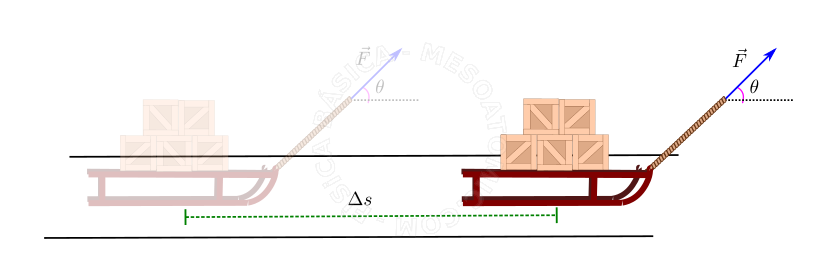
La unidad de trabajo, en el sistema internacional, es el Joule, \([W] = J\) .
Es importante que tenga en cuenta que el trabajo no es una cantidad vectorial, y si una grandeza escalar.
Es posible encontrar las siguientes fórmulas para el trabajo de diferentes fuerzas mecánicas:
- Trabajo del peso \((W_p)\) o fuerza gravitatoria.
- El trabajo para desplazar \(\Delta h\) un cuerpo de masa \(m\) en el campo gravitacional de aceleración \(g\) es: $$ W_p(h) = mg \Delta h$$ Tenga en cuenta que este trabajo solamente depende de la posición vertical (altura).
El peso no realiza trabajo en la horizontal! - Trabajo de la fuerza elástica \((W_e)\)
- El trabajo requerido para estirar un resorte, de constante de elasticidad \(k\), desde su posición de reposo \(x`\) a una posición \(x\) es: $$ W_e(\Delta x) = k \frac{(\Delta x)^2}{2},$$ donde \(\Delta x = (x`-x)\) .
- Trabajo de una fuerza cualquier \((W)\)
- Es el área bajo la curva de un gráfico de la fuerza por el desplazamiento, donde la fuerza en cuestión debe ser tangente a la trayectoria.
El Trabajo y el tiempo
En el caso de las máquinas, es interesante para medir la cantidad de trabajo que son capaces de producir por unidad de tiempo, esta cantidad se conoce como potencia. Por lo que es posible saber cuánto tiempo se necesita una máquina para producir el trabajo deseado.
Otra variable importante es el rendimiento, puesto que para que una máquina realice trabajo, primero es necesario suministrar energía a la máquina, es decir, la capacidad para realizar trabajo. Siempre hay una pérdida en este proceso. El costo beneficio de este proceso está dada por el rendimiento o eficiencia.
Las cantidades anteriormente pueden ser definidos como sigue:
- Potencia \((P)\)
- Es el trabajo realizado por unidad de tiempo, $$ P = \frac{W}{\Delta t},$$ y tiene la unidad de \(SI\) Watt, \([P]=W\) .
- Eficiencia \((\eta)\)
- Es la relación entre la potencia util \(P_u\) y la potencia total \(P_t\) , $$ \eta = \frac{P_{u}}{P_{t}}.$$ Esta cantidad es adimensional. Como potencia útil no puede ser nunca mayor que la potencia total suministrada al sistema, \(\eta\) está en el intervalo \([0,1]\) . Un buena maquina tiene una eficiencia cerca de 1 y mala máquina tiene una eficiencia pobre cercana al 0.
