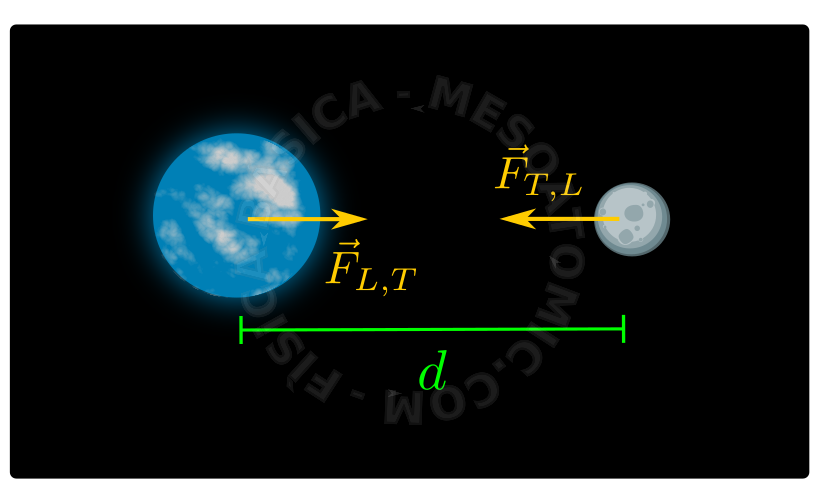
Considerando las dos masas representadas en la figura anterior: una de masa \(M\) y la otra de masa \(m\), separadas por una distancia \(d\), ocurrirá entre estas una atracción gravitatoria cuya intensidad es: $$ F = G\frac{ M m }{d^2},$$ donde \(G\) es una constante de valor \(6.67 \times 10^{-11} N(\frac{m}{kg})^2\). La dirección de esta fuerza está dada por una línea recta que conecta el centro de los objetos. Y donde los sentidos son opuestos debido a la tercera ley de Newton, como se muestra en la figura.

Leyes de Kepler

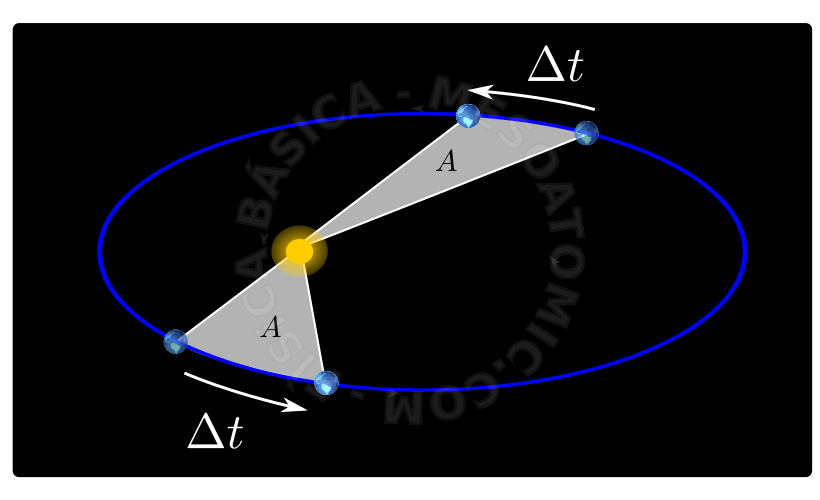
Debido a la atracción que los cuerpos celestes ejercen entre sí, las siguientes leyes fueron descubiertas por Kepler:

\(1^a\) - Ley de órbitas elípticas

Los planetas describen trayectorias elípticas, donde el sol ocupa uno de los focos de la elipse.

\(2^a\) - Ley de las áreas

El área barrida por el radio vector de un planeta genera áreas iguales en tiempos iguales (ver figura anterior).

\(3^a\) - Ley de los períodos

Los cubos de los radios promedio de los planetas alrededor del sol son proporcionales a los cuadrados de los períodos de revolución. O matemáticamente: $$ R^3 = k \tau^2,$$ donde \(R\) es el radio medio, \(\tau\) es el período de rotación alrededor del sol y \(k\) es una constante.

Observación: Cuanto más alejado un planeta este del Sol (mayor el radio), mayor será su período de rotación alrededor del Sol ( mayor el \(\tau\) ).