- Mecánica
- /
- Dinámica
- /
- Las leyes de Newton
Una vez que se conocen las fuerzas que actúan sobre un objeto, es posible utilizar las leyes de Newton para entender si el cuerpo entrará en movimiento y determinar las características de esta dinámica.
Para la aplicación de las leyes de Newton, es necesario que el observador del sistema este en un sistema de referencia inercial, es decir, que este parado o en movimiento rectilíneo y uniforme. Referenciales acelerados requieren otra formulación. Inicialmente, para facilidad, se considera que el cuerpo sólo puede moverse sin girar (movimiento de traslación). No podemos con esta formulación, por ejemplo, considerar el movimiento de una bola que al desplazarse tambien rota. Por lo tanto, se dice que el cuerpo bajo análisis es tratada como una partícula.
Leyes de Newton
- \(1^a\) - ley de inercia
-
Si la fuerza resultante que actúa sobre un cuerpo es cero, el cuerpo sólo puede estar en reposo o de movimiento rectilíneo uniforme (MRU).
La ley de la inercia puede parecer no intuitiva. En la Tierra, los cuerpos permanecen en movimiento cuando hay actuación de una fuerza que supera las de fricción. No se observa algo que se mueve eternamente sin que una fuerza esté actuando. Pero en el espacio, donde no hay fricción, un cuerpo que no interactúa con ningún otro y ya se encuentra en movimiento, permanecerá en movimiento rectilíneo eternamente (MRU), como ilustra la animación arriba. - \(2^a\) - la ley fundamental de la dinámica.
- La aceleración adquirida por un cuerpo es directamente proporcional a la fuerza neta e inversamente proporcional a su masa. Que de forma matemática, se puede escribir como \(\vec{a} = \frac{\vec{F_r}}{m}\) o, de forma más conocida: $$ \vec{F}_r = m \vec{a},$$ donde \(\vec{F}_r\) es la fuerza resultante que actúa sobre el sistema de interés.
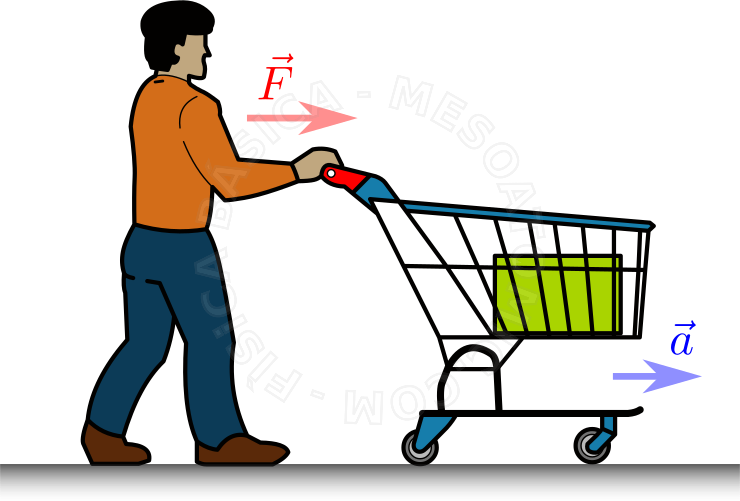
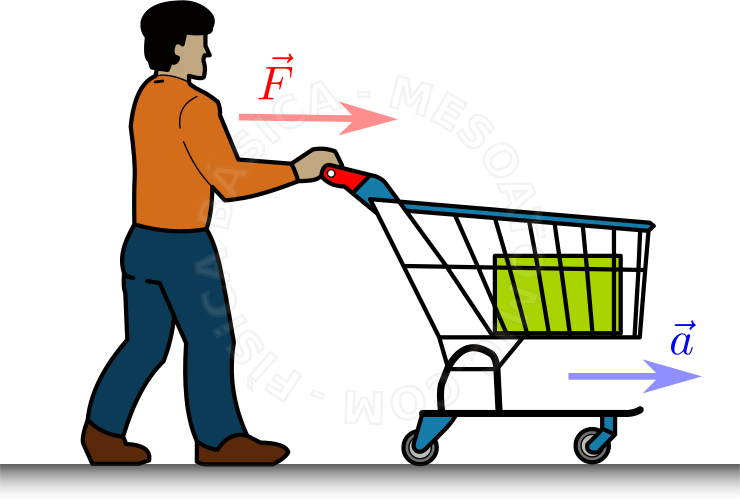

Las figuras ilustran los conceptos de la segunda ley. Considere diferentes carritos cargando bloques del mismo material, donde las fuerzas resultantes se etiquetan como \(\vec{F} \). Cada fuerza va a generar una aceleración, en la misma dirección de la fuerza. Al aumentar la fuerza, aumentamos la aceleración, como ilustra la segunda figura (observe el tamaño de los vectores). Sin embargo, si aumentamos la masa del carro y aplicamos la misma fuerza de la segunda figura, tenemos una aceleración menor. - \(3^a\) - ley de acción y reacción.
- A cada acción se tiene una reacción del mismo módulo y dirección, pero en sentido opuesto. En forma matemática: $$ \vec{F}_{a,b} = - \vec{F}_{b,a}, $$ donde \(\vec{F}_{a,b}\) es la fuerza que un cuerpo \(a\) hace en un cuerpo \(b\) .

Considere un nadador parado en una piscina. Para que el nadador se mueva hacia delante, empuja la pared hacia atrás, y como reacción, la pared empuja hacia adelante. Pero como los fluidos tienden a frenar objetos en movimiento (fuerza de arrastre), la tendencia natural es que el nadador vuelva al reposo. Pero, al nadar, el atleta continúa en movimiento, pues empuja el agua hacia atrás, y por reacción, el agua empuja al nadador hacia adelante.
