- Mecánica
- /
- Dinámica
- /
- Fuerzas de contacto
Las fuerzas de superficie, o de contacto, son esenciales para el análisis de los sistemas mecánicos, estas se dividen en dos componentes: las fuerzas normales y de fricción. 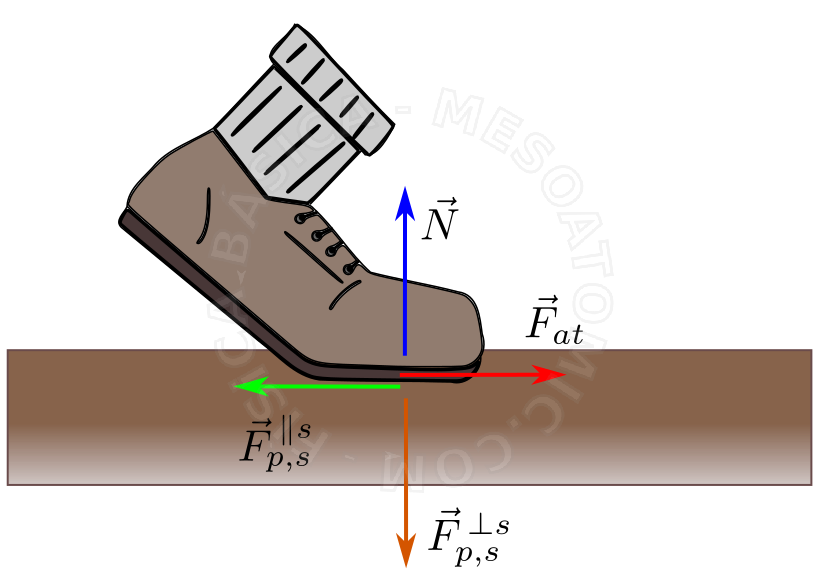
La figura anterior ilustra las fuerzas que actúan en el sistema pie y suelo . La fuerza normal \(\vec{N}\) que actúa sobre el pie, es la componente ortogonal de la fuerza de reacción que el pie ejerce en el suelo, \(\vec{N} = -\vec{F}_{p,s}^{\,\perp \, s} \). Ahora la fuerza de fricción \(\vec{F}_{at}\) es la componente paralela a la superficie de la fuerza de reacción que el pie hace en el suelo, \(\vec{F}_{at} = -\vec{F}_{p,s}^{\,\parallel \, s}\) .
Fuerzas normales
Una componente de fuerza que aparece en el contacto entre dos superficies es la llamada normal, que es siempre perpendicular, u ortogonal, a la superficie de contacto. Esta fuerza puede ser entendida de mediante la ley de acción y reacción, ya que cuando un objeto empuja la superficie de otro, este también será empujado con una fuerza de la misma intensidad en la misma dirección pero en sentido opuesto.
Características de las fuerzas normales
- Dirección
- Siempre ortogonal o normal a la superficie en el que el sistema de interés está en contacto.
- Módulo
-
El valor algebraico de la fuerza normal se puede encontrar utilizando la segunda ley de Newton. En el caso de un sistema de masa \(m\) que se mueva con aceleración \(a^{\, \perp \, s}\) perpendicular a la superficie de contacto \(s\), la ecuación para la fuerza normal es:
\(N + \sum_i^n F_i^{\, \perp \, s} = m \, a^{\, \perp \, s}.\) donde \( F_i^{\, \perp \, s}\) son los \(n\) valores algebraicos de las componentes perpendiculares a la superficie \(s\) de las otras fuerzas, que operan sobre el sistema. Importante: en esta ecuación es necesario considerar el módulo de componente con el signo algebraico indicando su dirección y sentido, es decir, el valor algebraico. La superíndice \((\perp \, s )\) es para llamar la atención que el cálculo de la fuerza normal sólo tiene en cuenta las fuerzas y aceleraciones perpendiculares a la superficie.
Fuerzas de fricción
La fuerza de fricción es el componente de fuerza de la superficie que es paralela a la superficie de contacto. Esta se manifiesta entre dos superficies de contacto donde está actuando una fuerza externa que tiene un componente paralelo a la superficie. Esta fuerza se divide en dos casos:
- Fricción estática
- Es la fuerza que actúa cuando hay una fuerza externa tratando de generar el movimiento entre las superficies, pero no hay movimiento relativo entre las superficies. El módulo máximo que esta fricción estática puede tomar es: $$F_{at(e)} \le \mu_e N,$$ donde \(\mu_e\) es una constante que depende de los tipos de materiales en contacto, y \(N\) es la fuerza normal en el sistema. Tenga en cuenta que la fuerza de fricción estática varía desde cero hasta el valor máximo . Esta fuerza sólo tendrá su valor máximo cuando la suma de las componentes de las fuerzas, que tienden a mover el objeto en una superficie dada, es igual a este valor máximo.
- Fricción cinética
- La fuerza de fricción cinética, o dinámica, actua cuando existe un movimiento relativo entre las dos superficies en contacto. El módulo de la fricción dinámica es siempre: $$F_{at(d)} = \mu_d N,$$ donde \(\mu_d\) es una constante que depende de los tipos de materiales en contacto, y \(N\) es la fuerza normal a la superficie de contacto.
Características de las fuerzas de fricción
- Sentido
- Es siempre opuesto al movimiento relativo entre las dos superficies, o a la tendencia del movimiento.
- Módulo
- Las fuerzas de fricción son proporcionales a la fuerza normal \(N\) , pero hay una gran diferencia entre el caso estático e cinético.
- Dirección
- Siempre tangente a las superficies de contacto donde se encuentra el sistema de interés.
- La irregularidad de las superficies en contacto.
- La atracción electromagnética entre las dos superficies en contacto.
