Cuando observamos un fenómeno en la naturaleza, podemos hacer esto desde diferentes lugares y maneras. Por ejemplo, al observar el movimiento de un automóvil, podemos observar el automóvil parado en una acera o podemos observar desde el interior de otro automóvil en movimiento. Sea como fuere, es importante que los análisis del movimiento sean consistentes, independientemente de cuál sea el referencial que observemos del movimiento.

La forma correcta de observar un fenómeno es adoptar un sistema referencial y un sistema de coordenadas. Por ejemplo, supongamos que se ha observado el mismo fenómeno a partir de dos referencias, identificadas por \(M \) y \(N \), donde el sistema \(N \) se mueve en línea recta en relación con el sistema \(M \), con velocidad relativa \(v_ {M, N} \). Siendo \(v_ {A, N} \) la velocidad de un automóvil \(A \), conocida en la referencia \(N \), podemos querer saber cuál es el valor de velocidad correspondiente \(v_ {A, M } \) del automóvil \(A \) en referencial \(M \). El concepto de movimiento relativo nos permite responder a este tipo de preguntas.

El movimiento relativo

La ecuación para el paso de una referencia a otra es conocido como transformación de velocidades de Galileo y tiene la siguiente forma: $$\vec{v}_{A,M} = \vec{v}_{A,N} + \vec{v}_{N,M},$$ donde \(\vec{v}_{A,M}\) es la velocidad \(A\) en la referencia \(M\) , \(\vec{v}_{A,N}\) es la velocidad \(A\) en la referencia \(N\) y \(\vec{v}_{N,M}\) es la velocidad de referencia \(N\) respecto de \(M\) .

Principio de independencia de los movimientos (Galileo)

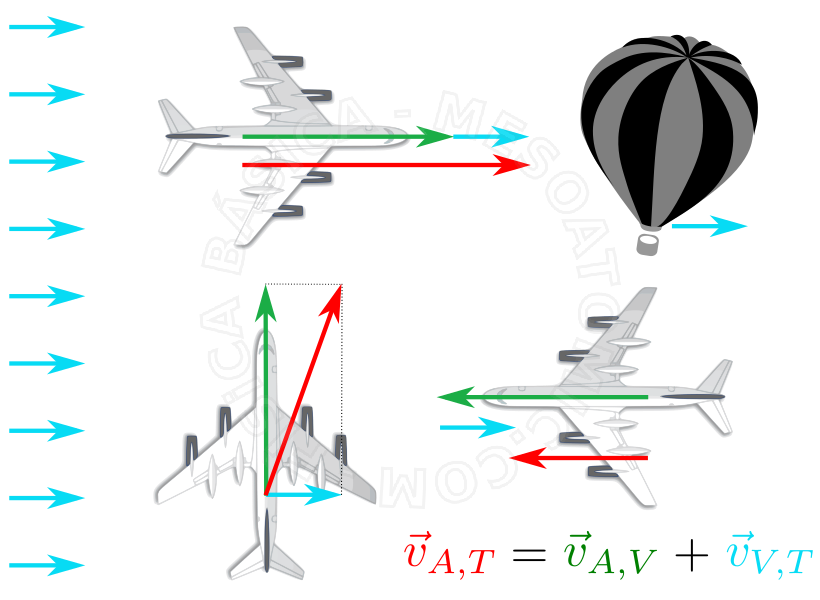
Cuando un cuerpo se encuentra bajo la acción simultánea de varios movimientos, cada uno de estos se procesa independientemente de los otros. La figura a continuación ilustra un caso típico de movimiento relativo.