- Física
- /
- Mecánica
Select the subtopic
Movimientos básicos

Considere un coche que se está derramando aceite, de modo que el aceite gotea en intervalos de tiempo iguales. Las posiciones de las marcas de aceite en la pista se pueden utilizar para...
Lanzamiento vertical

Lanzamiento vertical es el movimiento rectilíneo y vertical que un objeto describe cuando sólo esta sometido a la acción de la fuerza gravitacional, e donde se desprecia la resistencia del aire.
Cinemática vectorial

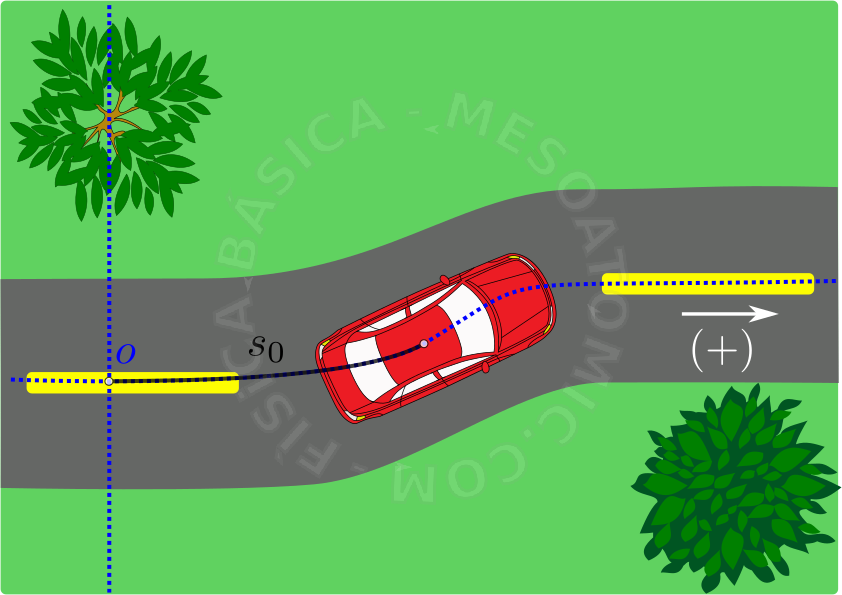
Cuando el movimiento se da en dos dimensiones o más, es necesario trabajar con vectores, es decir, se debe utilizar la cinemática vectorial. Un ejemplo de movimiento en dos dimensiones es un coche...
Movimiento circular

El movimiento circular es aquel cuya trayectoria describe un arco circular.
Movimiento relativo
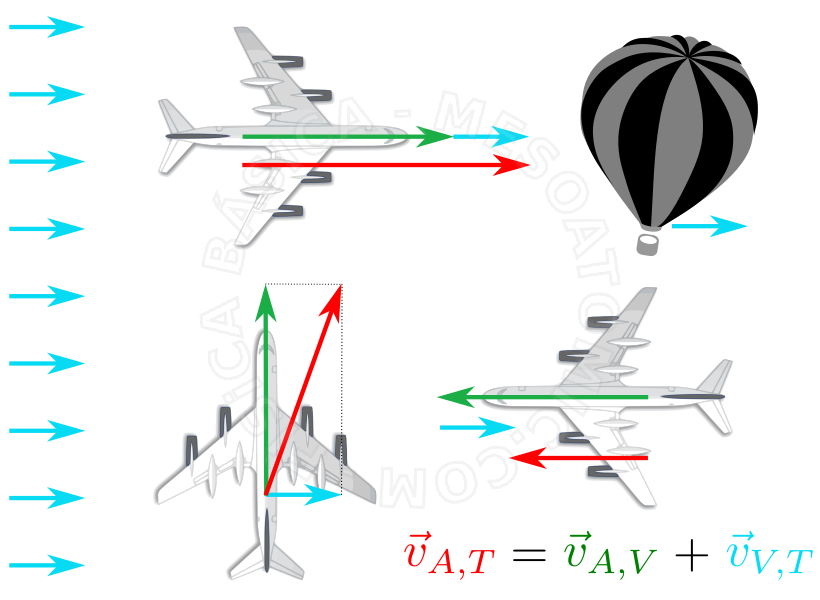
Cuando observamos un fenómeno en la naturaleza, podemos hacer esto desde diferentes lugares y maneras. Por ejemplo, al observar el movimiento de un automóvil, podemos observar el automóvil parado...
Movimiento de Proyectiles
Se llama lazamiento oblicuo el lazamiento de cualquier objeto cuya velocidad inicial forme en un ángulo distinto de \(90^0\) con la superficie de la Tierra .