- Fluidos
- /
- Hidrostático
- /
- Principios
Para describir el comportamiento de los fluidos en diferentes situaciones, es importante conocer los principios fundamentales.
Princípio Fundamental de la hidrostática (Princípio de Stevin)
La diferencia entre las presiones de dos puntos diferentes dentro de un líquido en equilibrio es proporcional a la densidad del líquido, \(\rho\) , el módulo de aceleración de la gravedad, \(g\) , y la diferencia en la altura de los puntos considerados \(h\) , matemáticamente, tenemos $$\Delta P = P_B - P_A = \rho g h.$$ 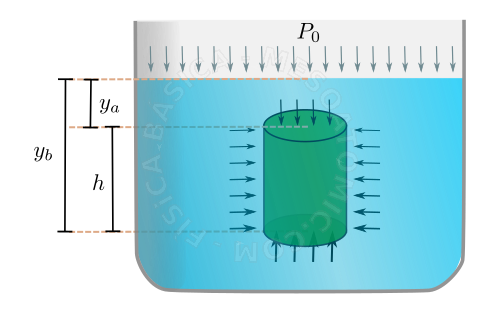
- la existencia de un campo gravitacional
- o debido a una aceleración del fluido por fuerzas externas (no gravitacionales)
- o debido a una combinación de ambas causas.
Es importante destacar que, en el caso del aire, ya que la densidad es muy baja, podemos ignorar la variación de la presión con el tiempo cuando esta variación es del orden de unos pocos metros.
Consecuencias del principio de Stevin
- Puntos que soportan la misma presión pertenecen a un mismo plano horizontal. Efecto: Toda la superficie libre de un líquido en equilibrio es horizontal.

Principio de los vasos comunicantes. No importa la geometría del recipiente, si el líquido puede pasar libremente de uno para otro, las líneas horizontas en estos recipientes tendran todas las mismas presiones, que aumentan con la profundidad ( \(P_h \gt P_0\) ) como establece el principio Stevin. - Cuando los líquidos inmiscibles (aquellos que no se mezclan) se colocan en un recipiente, estes se distribuyen de la parte inferior a la parte superior del recipiente, según el orden decreciendte de sus densidades; la superficie de separación entre dos líquidos inmiscibles es plana y horizontal.
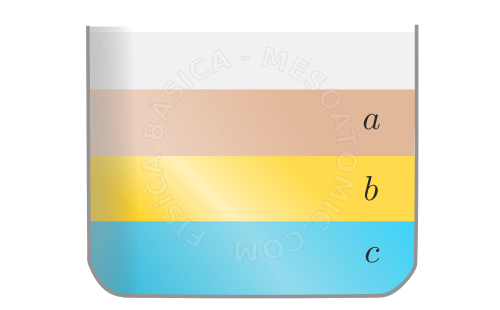
líquidos inmiscibles (que no se mezclan). La figura ilustra tres líquidos que no se mezclan, por ejemplo, líquido \(a\) podría ser agua, \(b\) aceite de cocina y \(c\) alcohol. - Si colocamos dos líquidos inmiscibles en un tubo en forma de "U", las alturas alcanzadas por los líquidos, considerando a partir de la superficie de separación, son inversamente proporcionales a las masas específicas de los líquidos, es decir $$ \frac{h1}{h2} = \frac{\rho_2}{\rho_1}.$$

líquidos inmiscibles en un tubo en forma de "U". En este caso, el líquido de color naranja tiene una densidad \(\rho_l\) que es menor que la densidad del líquido azul, \(\rho_a\) , por lo que esta en la parte superior. A pesar de las superficies en contacto con el aire (superficie libre) están a diferentes alturas, debido a la baja densidad del aire, se considera una buena aproximación que la presión atmosférica \(P_0\) es la misma en estos dos puntos. Con esto podemos relacionar las densidades de los líquidos con las alturas, asi: \(P_0 + \rho_l g h_1 = P_0 + \rho_a g h_2\) , es decir $$\rho_l h_1 = \rho_a h_2.$$
Ley de Pascal
Una variación de presión que se produce en cualquier punto de un líquido en equilibrio se transmite en su totalidad a todos los puntos de la red.
