El concepto de potencial eléctrico se relaciona a la medida de la cantidad de energía potencial \((E_p)\) adquirida por una carga unitaria al moverse en un campo eléctrico. (Análogo al potencial gravitatoria, que se refiere a la energía de desplazamiento de una masa en un campo gravitatorio.) Por definición, el potencial es un escalar.

El potencial eléctrico \(V_A\) en el punto \(A\) es igual al trabajo \(W_{A \rightharpoonup O}\) realizado por la fuerza eléctrica para llevar a una unidad de carga de punto de \(A\) al punto \(O\) (origen del potencial). La posición del punto \(O\) puede ser arbitrariamente escogida, en general, elegimos la posición que facilita el calculo en los problemas.

Para un conjunto finito de cargas, por convención se usa el origen del potencial, \(O\) , lejos de estas cargas (en el infinito), \( O \rightarrow \infty\) . Matemáticamente $$V_A = \frac{W_{A \rightharpoonup \infty}}{q},$$ es decir, el trabajo necesario para llevar una carga \(q\) desde el infinito hasta el punto \(A\) más cerca de las cargas generadoras del campo.

El potencial eléctrico en la unidad de SI es el Volt, \([V] = \frac{J}{C}\) (Joule por Coulomb).

El trabajo de la fuerza eléctrica \((W_{A \rightharpoonup B})\) :

El trabajo resultante de una carga eléctrica \(q\) en un campo eléctrico, que sufre un desplazamiento del punto \(A\) a el \(B\) , está dado por: $$ W_{A \rightharpoonup B} = q (V_B – V_A ),$$ donde \(V_A\) y \(V_B\) son los valores de potencial en los puntos \(A\) y \(B\) , respectivamente.

La energía potencial eléctrica \((E_p)\) :

Es la energía de una carga \(q\) en un punto \(A\), en presencia de un campo eléctrico externo. Es decir, es la energía del sistema formado por la carga y el campo externo donde ella está inmersa. Matemáticamente: $$ E_p(A) = q V_A$$ donde \(V_A\) es el potencial en el punto \(A\) . La unidad de \(E_p\) es el joule \((J)\) .

Diferencia de potencial:

La diferencia de potencial, \(ddp\), es igual al trabajo por unidad de carga, que un agente externo debe realizar para llevar una carga \(q\) en un campo eléctrico de \(A\) hasta \(B\), sin cambiar la energía cinética de la carga. Es decir, la diferencia de potencial \(U\) entre los puntos \(A\) y \(B\) es $$U_{AB} \equiv V_B – V_A = \frac{W_{A \rightharpoonup B}}{q} = \frac{E_p(B) - E_p(A)}{q}.$$ Por lo tanto, la \(ddp\) es también la diferencia de energía potencial eléctrica (Joule) por unidad de carga eléctrica (Coulomb) .

Potencial debido a una carga puntual:

El potencial de una carga electrica puntiforme \(q\) en un punto \(A\), en relación a un punto de referencia infinitamente lejos, está dada por: $$ V_A = k \frac{q}{d_A},$$ donde \(d_A\) es la menor distancia de la carga hasta el punto \(A\) . Una partícula de carga positiva produce un potencial eléctrico positivo y una negativa un potencial negativo.

Potencial eléctrico debido a un conjunto de cargas puntuales:

El potencial debido a un conjunto de cargas puntiformes, en un cierto punto en el espacio, es igual a la suma de los potenciales de cada carga.

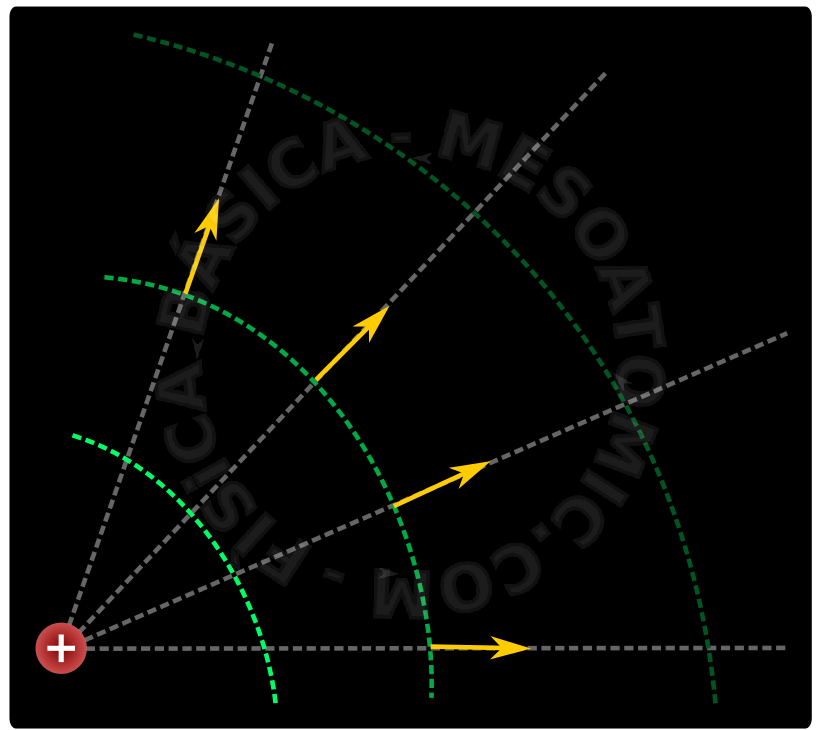
Las líneas de campo:

Las líneas de campo eléctrico apuntan en el sentido del potencial decreciente.

Electronvolt:

Es una unidad de energía comúnmente utilizada en la física atómica y nuclear. Es defina como la energía que un electrón o un protón adquiere al moverse a través de una diferencia de potencial \(1V\) , entonces \(1eV=1.6 \times 10^{-19} J\) .

Superficies equipotenciales

Superficies equipotenciales son las regiones del espacio donde el potencial siempre tiene el mismo valor y tienen las siguientes características:

• Los puntos sobre una superficie equipotencial tienen todos el mismo valor potencial de energía;
• El trabajo realizado sobre una carga de prueba, para moverla de una superficie determinada a otra es independiente de la ubicación de los puntos inicial y final sobre ellos y de la trayectoria que une los puntos;
• El campo eléctrico es siempre perpendicular a las superficies equipotenciales.