- Electromagnetismo
- /
- Electromagnetismo
- /
- Fuerza magnética
A diferencia de otras interacciones, las fuerzas entre dos cargas en movimiento tienen ciertas peculiaridades: no son iguales en módulos, no tienen la misma dirección y tampoco son opuestas en sentido. Tenga cuidado al hacer analogías con las fuerzas de otras fuentes que usted ha estudiado.
La fuerza magnética
- Elemento de corriente
- Los electrones en movimiento forman una corriente eléctrica. Se llama elemento de corriente, a la cantidad de cargas eléctricas que atraviesan ortogonalmente alguna porción del conductor en algún intervalo de tiempo. La dirección de este vector es la misma que la del desplazamiento de cargas. La unidad de intensidad de corriente eléctrica en el SI es Ampere \((A = \frac{C}{s})\) .
- La permeabilidad magnética \((\mu)\)
- Es una constante de proporcionalidad, que depende del material del objeto estudiado. Se utiliza para calcular la fuerza que actúa sobre un elemento de corriente en presencia de un campo magnético. La permeabilidad de vacío (ausencia de material) representada por \(\mu_0\) , es: $$\mu_0 = 4 \pi 10^{-7} \frac{Tm}{A}$$ recordando que \(\pi\) vale aproximadamente 3.14.
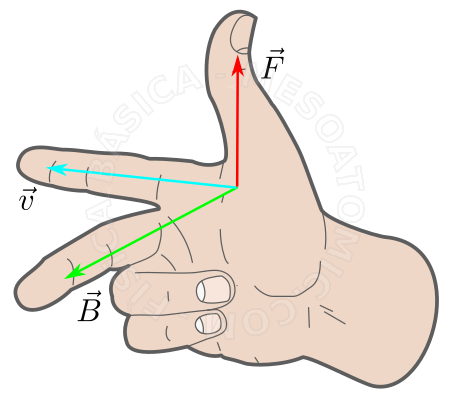
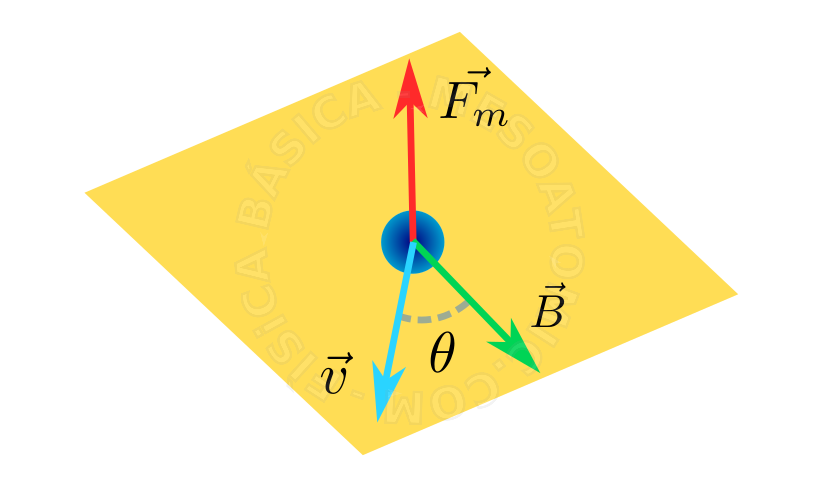
Fuerza de Lorentz
Es la fuerza magnética \(\vec{F_m}\) que actúa sobre una partícula electrificada con carga positiva \(q\) cuando la partícula se mueve con velocidad \(\vec{v}\) en la región de un campo magnético \(B\) . Esta fuerza tiene las siguientes características:
- Dirección
- Perpendicular al plano determinado por \(\vec{v}\) y \(\vec{B}\) .
- Sentido
- Viene dada por la "regla de la mano derecha". Y si la carga \(q\) fuera positiva, el sentido de la fuerza es contrario a la obtenida por la regla si la carga fuera negativa;
- Intensidad
- Viene dada por: $$F_m = qv B ~sen(\theta)$$ donde \(\theta\) es el ángulo entre el vector \(\vec{v}\) y \(\vec{B}\) .
Aplicaciones de la fuerza magnética
- Cargas en un campo magnético
- Una carga en movimiento en un campo magnético uniforme experimenta una fuerza que es perpendicular a la velocidad. La trayectoria de esta carga será una circunferencia y la fuerza centrípeta es la propia fuerza magnética. En el caso de una partícula cargada de masa \(m\) y carga de valor absoluto \(|q|\), moviendose con velocidad \(\vec{v}\) perpendicular a un campo magnético uniforme \(B\), el radio de la trayectoria circular será: $$r = \frac{mv }{ q B}$$
- Conductor en un campo magnético
- Para un conductor lineal, de longitud \(L\), recorrido por una intensidad de corriente \(i\), inmerso en un campo magnético uniforme \(\vec{B}\), con \(\theta\) siendo el ángulo entre el conductor y \(\vec{B}\), la fuerza magnética está dada por: $$F_m = i BL ~ sen(\theta)$$
- Fuerza entre conductores
- Considere un cable largo, recorrido por una corriente eléctrica. Considere un elemento de corriente en el entorno de este cable y paralelo a este. Se encontró experimentalmente que el elemento de corriente está sujeto a la acción de una fuerza que tiene las siguientes características:
- 1
- La fuerza es atractiva, si los sentidos de la corriente que fluye a través del alambre y el elemento de corriente son iguales, y es repulsiva cuando estos sentidos son opuestas;
- 2
- La intensidad de la fuerza es directamente proporcional al producto de la intensidad de la corriente que fluye a través del alambre por el módulo de elemento de corriente e inversamente proporcional a la distancia que los separa.
Regla de la mano derecha