- Electromagnetismo
- /
- Electrodinámica
- /
- Resistencia electrica
En un circuito eléctrico, la componente que se opone al paso de la corriente eléctrica se llama resistencia eléctrica o resistencia.
Resistencia eléctrica
Definiciones importantes:
- La resistencia eléctrica \((R)\) :
- Un elemento resistivo de un circuito se dice ómhico si la resistencia de este no depende del voltaje, ni de la dirección o de la intensidad de la corriente (Ley de Ohm). Para estos elementos, la resistencia eléctrica es la relación constante entre la diferencia de potencial \(V\) entre los terminales de conductor y la intensidad de la corriente \(i\) que pasa a través de él, es decir: $$ R = \frac{V}{i}.$$ La resistencia eléctrica de un sólido depende básicamente de dos factores:
- 1) El número de electrones libres en su estructura;
- 2) De la movilidad de los electrones libres al moverse a través de la red de moléculas del sólido.
- Ohmímetro:
- Es el instrumento utilizado para medir la resistencia eléctrica.
Ley de Ohm
Un conductor obedece a la ley de Ohm si el valor de su resistencia es independiente de la diferencia de potencial \(V\) y de la corriente \(i\) aplicada. Es decir, la caída de potencial \(V\) a través de una resistencia óhmica \(R\) que es atravesada por una corriente \(i\) viene dada por: $$V = R i$$ La ley de Ohm es una ley empírica y vale para algunos materiales. En general, los conductores metálicos son óhmicos, pero otros pueden no ser, como los gaseosos o líquidos y otros dispositivos electrónicos, tales como transistores y diodos. Para estos últimos, el gráfica de la variación \(ddp\) con la intensidad de la corriente no es lineal. Sin embargo, podemos afirmar que para las pequeñas variaciones de \(ddp\) casi todos los conductores de la naturaleza obedecen la Ley de Ohm.
Resistividad \((\rho)\)
Para un hilo conductor de un material de resistividad \(\rho\) , su resistencia eléctrica es directamente proporcional a su longitud \(L\) e inversamente proporcional al área \(A\) de su sección transversal, de manera que $$ R = \rho \frac{L}{A}.$$ 
Otras magnitudes similares a la resistividad son:
- Conductancia \((G)\)
- Es el inverso de la resistencia eléctrica $$G = \frac{1}{R}.$$ La unidad de la conductancia eléctrica es Siemens \((S)\) , y \(S = \frac{1}{\Omega}\) .
- Conductividad \((\sigma)\)
- Es la inversa de la resistividad, $$ \sigma = \frac{1}{\rho}.$$
Componentes resistivos (resistencia)

- a) generadores de calor (planchas eléctricas, hornos)
- b) la limitación de la corriente eléctrica,
- c) divisores de tensión.
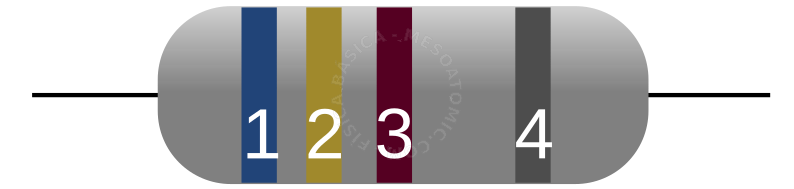
| Color | 1er díg. | 2do dig. | multiplicador | toleráncia |
|---|---|---|---|---|
| Sin | - | - | - | 20% |
| Plata | - | - | \(10^{-2}\) | 10% |
| Oro | - | - | \(10^{-1}\) | 5% |
| Negro | - | 0 | \(10^{0}\) | - |
| Marrón | 1 | 1 | \(10^{1}\) | 1% |
| Rojo | 2 | 2 | \(10^{2}\) | 2% |
| Naranja | 3 | 3 | \(10^{3}\) | - |
| Amarillo | 4 | 4 | \(10^{4}\) | - |
| Verde | 5 | 5 | \(10^{5}\) | 0,5% |
| Azul | 6 | 6 | \(10^{6}\) | |
| Violeta | 7 | 7 | \(10^{7}\) | |
| Gris | 8 | 8 | \(10^{8}\) | |
| Blanco | 9 | 9 | \(10^{9}\) |
Variación de la resistencia con la temperatura
Para que un conductor obedezca la ley de Ohm, dependerá de cómo su resistencia varía con la temperatura. Una vez que haya un aumento de temperatura: aumentará la vibración de las moléculas del material y será mayor el número de choques entre los portadores de carga y moléculas. Con esto la resistencia aumenta.
Un material de resistencia \(R_0\) a una temperatura \(t_0\) tendrá una resistencia mayor \(R\) al someterse a un cambio de temperatura \(t - t_0\) . Para muchos materiales de la relación entre la temperatura y la resistencia viene dada por la ecuación $$R=R_0[1+\alpha(t-t_0)],$$ donde \(\alpha\) es el coeficiente de variación térmica de la resistencia del conductor.
