- Undulatory
- /
- Simple Harmonic Motion
- /
- Spring-mass and S. pendulum
The simple harmonic oscillator is an isolated system; that is, it has no external forces. In addition, there is no damping at all. It is also known as mass-spring system. In this system, the only acting force is the elastic force of the spring.
Simple Harmonic Oscillator
This system has the following characteristics:
- The spring-mass system performs simple harmonic motion (SHM)
- The elongation in the SHM is, in module, the deformation (distension or contraction) of the spring.
- When the weight and the normal force are perpendicular to the movement, and friction is negligible: the resultant force on the body comes only from the spring force.
- At the equilibrium position, the spring force is null and the spring is not deformed.
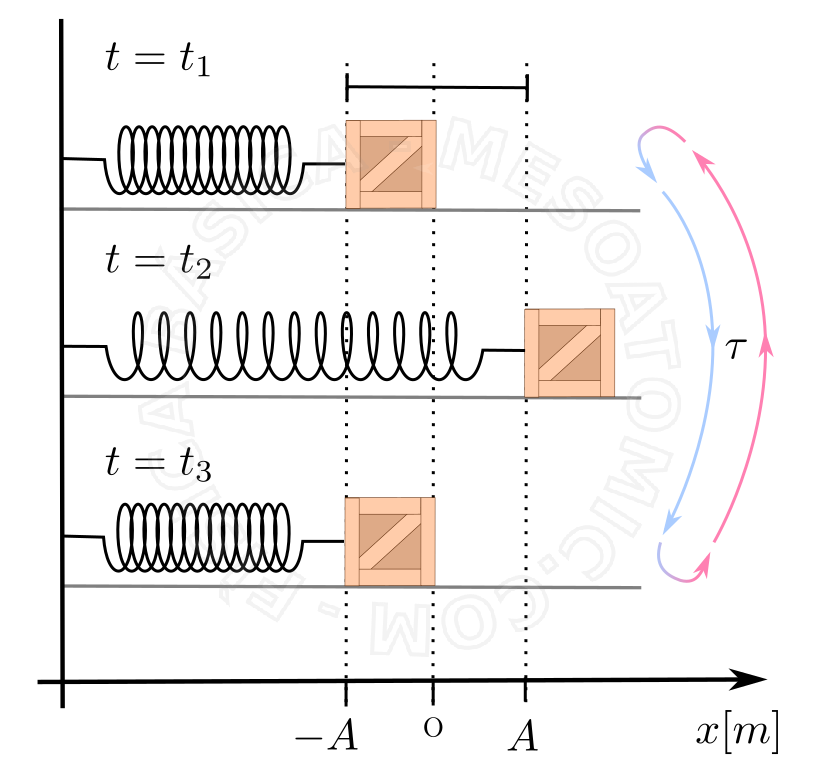
\(t_1\): the spring is compressed and pushes the block
\(t_2\): the spring reaches its maximum stretch and the block starts the return movement to its initial position (the spring is pulling the block).
\(t_3\): the block returns to its original position completing an oscillation (the spring makes no force on the block). If frictionless, this motion will be repeated indefinitely.
The letter \(\tau\) stands for the time the block takes to perform a complete oscillation and \(A\) is the amplitude of the movement.
Energy
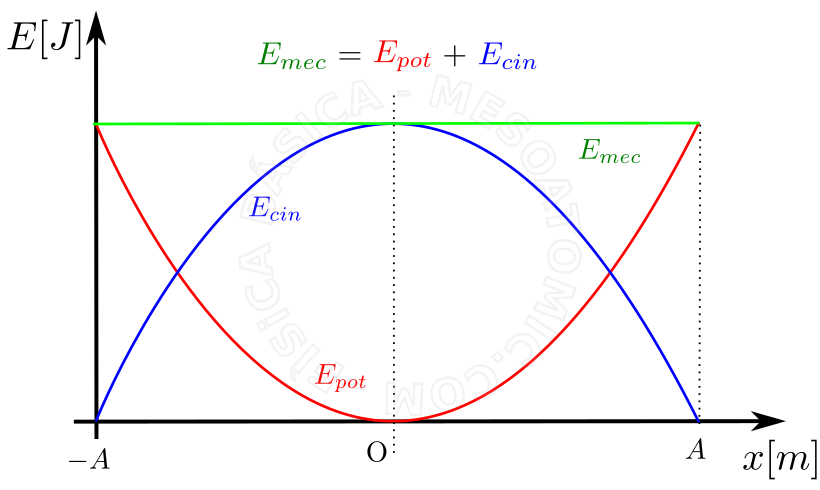
Given a mass-spring system or other simple harmonic oscillator, where frictional forces are neglected, there will be conservation of mechanical energy; that is, for any system configuration the sum of the kinetic energy plus the potential is constant. In the case of mass-spring system, we have:
- \( E_k = m \frac{v^2}{2} \)
- \( E_{e} = \frac{kx^2}{2} \)
- \( E_{mec} = E_k + E_{e} = \frac{k A^2}{2} = \text{Constant} \)
Association of Springs
Imagine we have two bodies, \(A\) and \(B\), and we want to hold more than one spring between them. We call it "Serial Association" when we join the springs one after the other, in a row. When in parallel, each spring is connected in parallel between \(A\) and \(B\).
In the calculation, we can replace all the elastic constants for an equivalent one, depending on the configuration:
- Series association:
- \( \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} .\)
- Parallel association:
- \( k_{eq} = k_1 + k_2 .\)
The simple pendulum
It is a device consisting of a particle of mass \(m\) suspended by a rod (string or wire) of negligible mass and length \(L\). In old clocks (upper-case clocks) simple pendulums are used to mark the flow of time. The pendulum behaves like a harmonic oscillator when the vibration amplitude is small in relation to the length \(L\) (small angles).
Period of a simple pendulum
Considering friction is negligible, through the Newton's laws, it is possible to deduce the period of the simple pendulum for small angles, that is: $$ \tau = 2 \pi \sqrt{\frac{L}{g}},$$ where \(g\) is the acceleration of gravity and \(L\) is the pendulum length. This period has the following properties:- It depends only on the length of the pendulum and the local acceleration of gravity.
- It does not depend on the pendulum mass.
- It is isochronous, that is, the period does not depend on the amplitude.

