- Thermophysics
- /
- Thermodynamics
- /
- Gas study
"The universe is modeled as a gas."
Macroscopic View of Gases
Gases are formless fluids, easily compressible that tend to occupy the full volume of the container containing them. In an idealized microscopic view, we have:
- Gases are made up of molecules.
- The forces of attraction between the molecules of the gas can be ignored.
- The volume occupied by the gas molecules is negligible when compared to that of the container containing it.
- The motion of the gas molecules is continuous and random.
A Model of Real Gases: The Ideal Gas
In order to study the real gases we use an ideal model called the ideal gas, which models a real gas of difficult liquefaction, in low pressure and in high temperature. For the study of gases, the following are very important:
- The Avogadro's Law
- It says that equal volumes of gases, under the same conditions of temperature and pressure, have the same number of molecules. Since the number of molecules of a gas is a very large number, we refer to the number of molecules as a multiple of a very large number called mol. It's just a name of a fixed quantity, a "very big dozen."
- 1 Mole of Any Gas
- It is at the temperature of 0°C and 1 atm pressure, occupies the volume of 22.4 liters and contains \(6.023 \times 10^{23}\) molecules.
- Avogadro's number \((N_0)\)
- It is the number $$N_0 = 6.023 \times 10^{23},$$ that facilitates communication and the writing of the number of molecules in a gas. It is much easier to say that in a gas cylinder has 1 mol than to say that there are 602,300,000,000,000,000,000,000 molecules.
- STP - Standard Temperature and Pressure Conditions
- It refers to a temperature of 0°C and 1 atm.
State Equation of an Ideal Gas
Each steady state in which a gas is presented can be characterized, from the macroscopic point of view, by the following macroscopic properties:
- Pressure \((P)\)
- Volume \((V)\)
- Temperature \((T)\)
In an ideal gas, the above variables are related through the state equation: $$PV = n RT,$$ where \(n\) is the number of moles of gas and \(R\) is the universal constant of the perfect gases and $$R = 0.082 ~ atm \cdot l/mol \cdot K \\ = 8.31 ~J/mol \cdot K.$$
It is extremely important to note that this equation does not tolerate other temperature scales. Only temperatures in Kelvin can be used. If we have measurements in Celcius or Fahrenheit, we must first transform it to Kelvin.
Combined Gas Law
The perfect gas law helps us calculate what will happen after a transformation takes place in the gas. See the figure below.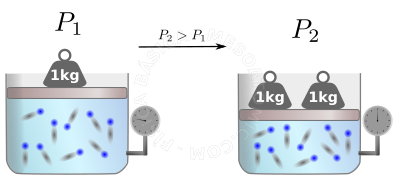
Gas transformation
Gases undergo state transformations when they produce work on a machine; that is, they go from an initial state to an end state. These transformations can occur in several ways. Some of them are:
- Isobaric process
- It occurs at constant pressure, then $$P_1 = P_2 \Rightarrow \frac{V_1}{T_1} = \frac{V_2}{T_2}.$$
- Isothermal transformation
- It occurs at constant temperature, then $$T_1 = T_2 \Rightarrow P_1.V_1 = P_2.V_2.$$
- Isochoric process (isovolumetric)
- It occurs at constant volume, then $$V_1 = V_2 \Rightarrow \frac{P_1}{T_1} = \frac{P_2}{T_2}.$$
- Adiabatic transformation
- It occurs without heat exchange between the gas and the medium, then $$Q_1 = Q_2.$$
Work on Gas Changes
Unlike what is studied in mechanics, the work of a gas depends on the initial state, the final state and also the path of transformation. The work performed by the gases in different transformations are described below.
- Isobaric process (\(P = \text{Constant}\))
- The work \(W\) carried by a gaseous mass in an isobaric process (\(P = \text{Constant}\)), which had a volume change \(\Delta V = \text{'final volume'} - \text{'initial volume'}\) is $$W = P \cdot \Delta V.$$
- Any transformation
- The work done on a gas mass during any processing is numerically equal to the area under the curve in the graph \(P \times V\) (see chart below). For different transformations the work assumes different signs, such that:
- Expansion
- \(V_f \gt V_i \Rightarrow \Delta V \gt 0 \Rightarrow W \gt 0 \).
- Compression
- \(V_f \lt V_i \Rightarrow \Delta V \lt 0 \Rightarrow W \lt 0. \)
- Constant volume
- \(V_f = V_i \Rightarrow \Delta V = 0 \Rightarrow W = 0 \).
- A positive work can be interpreted as the work done by the gas.
- A negative work can be interpreted as the work done on the gas.
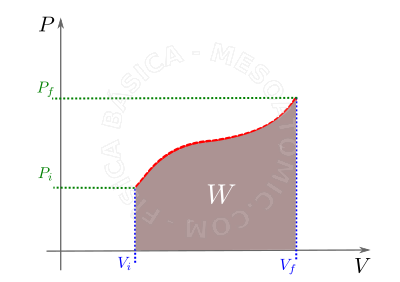
Work done by a gas. For a gas undergoing a transformation that its pressure and volume will vary with a given function (red line), the work will be given by the area under this curve (brown area). - Cyclical Transformation
- It is the transformation in which, after its course, the final conditions of pressure, volume and temperature are the same as the initial ones, and the area bounded by the cycle in the diagram \(P \times V\) measures the work done on it. See figure below.
-
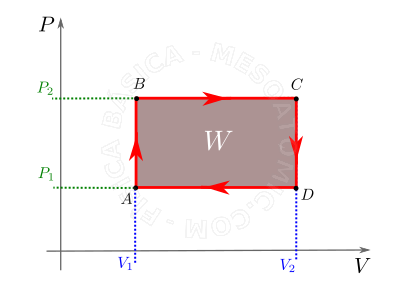
Cyclical transformation. To a cyclic processing as red lines illustrate the work done is the area inside the loop, brown area. By convention, the work done is positive if the cycle is traversed clockwise, and negative if it is traversed in an anti-clockwise.
