- Thermophysics
- /
- Thermodynamics
- /
- First law of thermodynamics
"The total energy of the universe is unchanging."
At the beginning of the development of thermodynamics, it was applied to problems involving the transformation of heat into work. Nowadays, thermodynamic methods are applied in multiple physical and chemical transformations, for the study of the properties of substances and of radiation.
Thermodynamics
- System, Surroundings and Boundary.
- A bounded region of space to be studied is called "system" and is separated from the rest of the universe ("external environment" or "surroundings") through a real or imaginary surface called the "boundary".
-
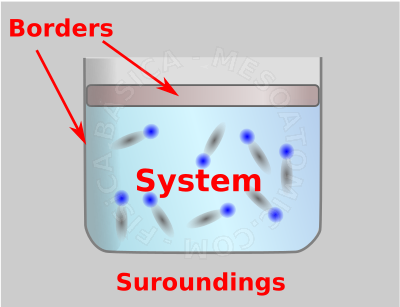
Thermodynamic system. The figure shows a gas inside a container. If we consider that the gas is the system of interest, then, the container will be the boundary of this system and everything else will be considered surroundings. - Thermodynamic State
- The microscopic thermodynamic state of a system is characterized by its internal energy. The macroscopic thermodynamic state is characterized by a set of macroscopic quantities called state variables (pressure, volume, temperature, number of moles, etc.). The variables required to determine the internal energy of a system are obtained experimentally.
- Transformation
- When there is a change in the thermodynamic state of a system, we say that there was a transformation. The way the transformation happens is called "process."
- Internal Energy
- It is the sum of the kinetic energies of all its constituent particles plus the sum of all potential energies arising from the interactions between the particles of the system. (Note: The internal energy does not include the potential energy arising between the system and its surroundings.) The internal energy variation of an ideal gas does not depend on the process. It depends only on the initial and final temperature of the same.
- External Energy
- The energy exchanged by the system and the external environment. The exchange can be on the form of heat or work, and depends on the transformation process.
- State Function
- They are functions whose values depend only on state variables, that is, variables that depend only on the actual thermodynamic state of the system.
-
First Law of Thermodynamics
- The first law is essentially an extension of the principle of energy conservation in order to include systems where there is heat flow. Historically, it marks the recognition of heat as a form of energy (Joule experience). The first law applies to any and all natural processes that take place between states of equilibrium.
- Definition of the Law:
- When an amount of heat \(Q\) is supplied to a system during a process, part of it \(\Delta U\) stays in the system as internal energy and part \(W\) leaves the system in the form of work done by the system on its neighborhood. Mathematically we have: $$\Delta U = Q - W.$$
-
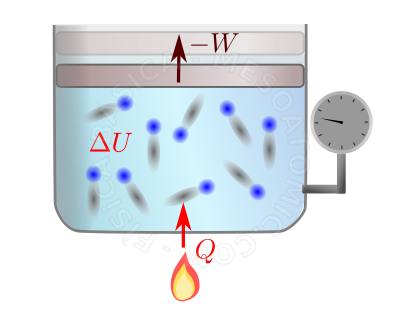
First Law of Thermodynamics. The figure illustrates a gas being heated by a flame and expanding (the upper vector illustrates the displacement of the plunger of the vessel). When thermal energy (heat) is received, the molecules of the gas get agitated (\(\Delta U\) increases). With this, there are more collisions between the gas and the plunger, causing it (the plunger) to move. For this motion, it is necessary for the gas to perform work on the plunger. Thus, the gas losses some energy. On the other hand, the plunger does work on the system surroundings (in this case, on the gas/air surrounding the system), giving this energy to the surroundings.
Applications of the First Law of Thermodynamics
Depending on the transformation a substance undergoes, the specific heat (and thermal capacity) of the substance changes. To describe the thermodynamic transformation of an ideal gas, we need to consider the specific heat at constant pressure \(c_p\) and constant volume \(c_v\). It is possible to relate these two quantities:
- Poisson's Ratio
- It is possible to relate the thermal capacities by: $$\gamma = \frac{C_p}{C_v} = \frac{c_p}{c_v}.$$ We have the following values for \(\gamma\) :
\(\frac{5}{3} = 1.67\) for monatomic gases
\(\frac{7}{5} = 1.40\) for diatomic gases (usually, this is a good approximation for the air). - Mayer's Ratio:
- $$c_p - c_v = R,$$ where \(c_p\) is the specific heat at constant pressure and \(c_v\) is the specific heat at constant volume.
Now we will see the gas transformations.
- Cyclical change
- In a cyclic transformation, the system always returns exactly to its initial state, therefore: $$\Delta U = 0,$$ $$W = Q.$$
- Isocoric (or Isovolumetric) Transformation
- They are transformations that happen at constant volume: (\(V = \text{Constant}\)). The heat exchanged is given by $$ Q = m c_v \Delta T,$$ the work is $$ W = 0,$$ and the variation of internal energy is $$ \Delta U = m C_v \Delta T,$$ where \(m\) is the mass of gas and \(\Delta t\) variation in temperature.
Example: pressure cooker - Isobaric Process
- They are transformations that happen at constant pressure ( \(P = \text{Constant}\) ). When this process occurs, the heat exchanged and the work done are both different from zero. The work done is equal to the pressure times the variation of volume: $$W = P \Delta V.$$ As heat is exchanged: $$Q = m C_p \Delta T,$$ we have $$\Delta U = m C_p \Delta T - P \Delta V$$ Example: Open-air processes are at constant atmospheric pressure.
- Isothermal Transformation
- They are transformations at constant temperature (\(T = \text{Constant}\) ). $$\Delta U = 0 \Rightarrow Q = W $$ $$W = n RT~\ln \left(\frac{V_f}{V_i}\right)$$ where \(ln~x = log_e~x\).
- Adiabatic Transformation
- It is a transformation where there is no heat exchange with the external environment \((Q = 0)\). The work of this transformation is: $$\Delta U = -W = m C_v \Delta T.$$ Example: Rapid reactions where there is insufficient time for significant heat exchange or when the system is thermally isolated from the external environment through adiabatic boundaries.
- Adiabatic Free Expansion
- The initial and final internal energy of a gas are equal, when the gas undergoes a free adiabatic expansion. $$T_0 = T_1$$ $$P_0 \cdot V_0 = P_1 \cdot V_1$$
- Boiling Process
- Suppose a liquid of mass \(m\) is vaporized at constant pressure \(P\). The volume of the liquid is \(V_l\) and the volume in the vapor state is \(V_v\). $$W = P (V_l - V_v)$$ $$\Delta U = Q - W = m L_v - P (V_l - V_v).$$
