- Thermophysics
- /
- Temperature
- /
- Dilatation of solids
Thermal expansion is the phenomenon where changes in the volume of a body is caused by variation of its temperature. It generally occurs due to the increase in the degree of agitation of its molecules and thus there is an increase in average distance between them.
Dilatation of Isotropic Solid
- Volumetric Expansion
- Objects in which the three dimensions are of the same order, often vary significantly in these dimensions. That is, you cannot neglect any variation. Some examples are: cubes, parallelepiped and others. For this class of objects, we must use the volumetric expansion, whose formula is: $$\Delta V = V_0 \gamma \Delta T,$$ where \(\Delta V = V - V_0\) is the volume change, \(\gamma\) is the coefficient of volumetric thermal expansion and \(\Delta T = T - T_0\) the temperature variation.
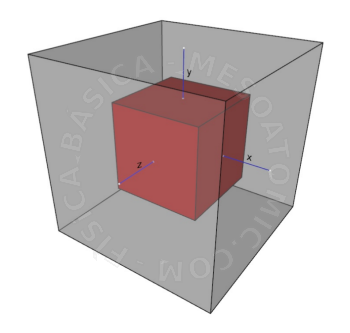
Illustration of volumetric expansion. Consider the red block in the figure. Heating the block will make it expand and occupy a new volume (transparent gray block). In this case the new volume, considering that its dimensions have doubled, will be \(\Delta V = 2x \cdot 2y \cdot 2z\) which is a multiplication of total variation in each dimension. - Superficial Dilatation
- Some objects have a very large surface area relative to their volume. Some examples are: sheets, plates and tiles. For this class of objects the thickness variation is usually negligible compared with the surface variation, so that the variation of the area \(\Delta A\) surface is given by: $$\Delta A = A_0 \beta \Delta T,$$ where \(A_0\) is the initial area, \(\beta\) is the surface's coefficient of expansion and \(\Delta T\) is the variation in temperature that the system has undergone.
- Linear Expansion
- Sometimes, only one of the dimensions of an object is of practical interest. When this is the case, we only study the variation in length of interest, and do not concern ourselves about the other two dimensions of the object. A practical example is the swelling suffered by a rail of a railroad. Although the height and thickness of the rails varies, only its length is of interest. If we do not take into account the rail's linear expansion during the construction of the railway, it may end up being deformed in a hot day. The formula for linear expansion is: $$\Delta L = L_0 \alpha \Delta T,$$ where \(\Delta L = L - L_0\) is the variation in length suffered after a temperature change \(\Delta T = T - T_0\), \(\alpha\) is the linear thermal expansion coefficient and \(L_0\) is the system's length before it suffers a variation in temperature.
- Relationship Between the Coefficient of Expansion for Isotropic Materials:
- $$\beta \approx 2 \alpha$$ $$\gamma \approx 3 \alpha$$ $$\beta \approx 2/3 \gamma$$
Coefficient of Linear Expansion Substance Value ( \(10^{-6} K^1\) ) Ice \(51\) Copper \(17\) Steel \(11\) Glass (common) \(9\) Glass (Pyrex) \(1.2\) Invar (iron + nickel) \(0.7\) quartz cast \(0.5\) Comments
From the dilatation point of view, the solids are considered isotropic when dilatations in different directions are proportionally equal. This does not occur for some crystals, which are called anisotropic, which dilatate proportionally more in one direction than in others.
Materials with smaller coefficients of expansion dilatate less for the same temperature variation.
In general, the coefficient of expansion varies with temperature, but in many practical cases it is possible to neglect this variation. This approximation is valid when we are interested in a temperature variation that is not very large and when the material does not approach its melting point.
