- Optics
- /
- Refraction, Lenses and Optical Inst.
- /
- refractive and refractive means
The speed of light changes when moving from one means to another
Refraction
The light refraction phenomenon is associated with the change of the speed of light when passing from one means to another. The speed of light changes in the refraction, i.e., in passing from one means to another.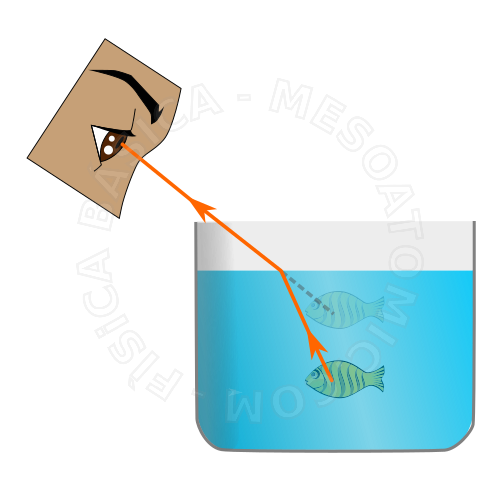
-
For the study of refraction, the following definitions are important:
- Diopter
- It is the set of two media separated by a refractive surface. The substances which constitute the transparent media are called refractive means. The higher the refrangibility of a means, the smaller will be the speed of light in this means.
- The Speed of Light in Vacuum \((c)\)
- It is \(300.000 \frac{km}{s}\) or \(3.10^8 \frac{m}{s}\). The speed of light in air is approximated to its speed value in vacuum.
- The Absolute Refractive Index \((n)\)
- It is the ratio of the speed of light in vacuum, \(c\) , and the speed of light in the means in question:
- \begin{equation} n=\frac{velocidade\ da\ luz\ no\ v\acute{a}cuo}{velocidade\ da\ luz\ no\ meio}\ = \frac{c}{v}. \end{equation} Examples of materials with different refractive indexes:
-
Substance \(n\) Pure water 1.33 Table salt 1.54 Diamond 2.42 Ethyl alcohol 1.36 Glycerin 1.47 Glass crown 1.52 Ice 1.31 Paraffin 1.43 - The Relative Refractive Index
- It is obtained from a means \(A\) in relation to another means \(B\) through the formula: \begin{equation} n_{ab}=\frac{n_{A}}{n_{B}}=\frac{v_{B}}{v_{A}}, \end{equation} where \(n_A\) is the mean's refractive index \(A\) and \(n_B\) is the refractive index of the means \(B\).
Refraction of Laws
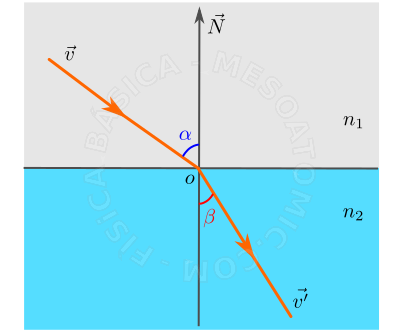
For a light ray incident on two means with different refractive interface indexes, the incident ray and the refracted one will not be in the same plane. The angles which these rays make with the normal vector of the interface between the means can be found at the law of Snell-Descartes, who says: "For a monochromatic beam of light passing from one means to another, the product of the angle's sine formed by the ray and the normal to the refractive index of the mean in which it is the radius is constant". Mathematically, we have: \begin{equation} n_{1} sen(\alpha) =n_{2} sen(\beta). \end{equation} Notice that when the light beam passes from one less refractive means (higher speed) for a more refractive means (slower) it approaches the normal, and vice versa. The figure below illustrates this phenomenon.
Total Reflection
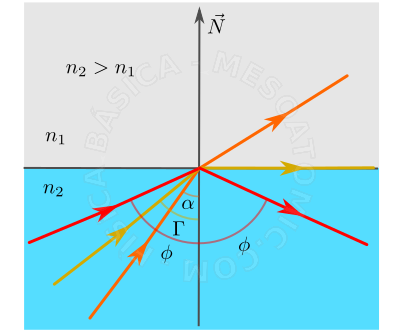
When light passes from a more refractive means to a less refractive one, there is a limit angle, such that for angles greater than this, the light beam cannot change means, so that the beam is completely reflected at the interface between the means. This phenomenon is important for applications such as fiber optics and telescopes. The limit angle \(\Gamma\) is defined as the incident angle which corresponds to an oblique emergency \(90^{o}\) when light propagates from the most refractive means for the less refractive one, i.e., \begin{equation} sen(\Gamma)=\frac{n_{1}}{n_{2}}\text{, para }n_{1} \lt n_{2}. \end{equation}
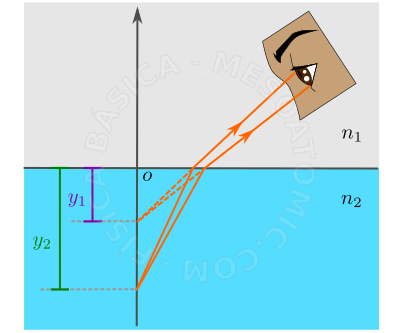
Diopter Plane
Blades of Parallel Faces
When a light beam crosses a parallel faced blade, it leaves the means with a given refractive index, let us say, \(n_1\) it passes through a means with index \(n_2\), and returns to the refractive means \(n_1\). Using the laws of refraction, we find that the emerging beam in refractive means \(n_2\) will be parallel to the incident beam in this means. See figure below.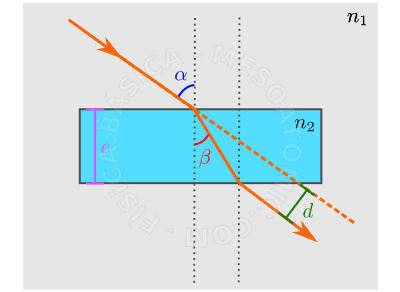
Prism
The optical system comprising three homogeneous and transparent media separated by two non-parallel planar surfaces is called prism.
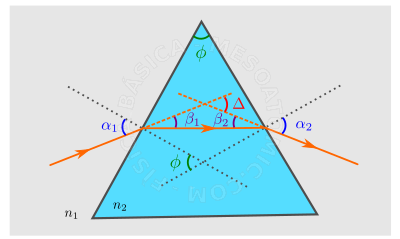
See figure above. For this system we can relate the angle between the two faces of the prism, \(\phi\) , with the angles with internal standard \(\beta_1\) and \(\beta_2\): \begin{equation} \phi = \beta_1 + \beta_2. \end{equation} It is also possible to find the angle that the incident ray in the prism will cause the beam to emerge from the material, \(\Delta\), i.e., \begin{equation} \Delta = \alpha_1 + \alpha_2 - \phi, \end{equation} where \(\alpha_1\) and \(\alpha_2\) are the angles that the light ray make with the external normals of the prism.
The analysis of optical prisms reveals that the deviation assumes the minimum value, \(\Delta_{min}\), when the angle of incidence in \(1^st\) face and emergency on \(2^nd\) face be equal ( \(\alpha_1 = \alpha_2\) ) such that: \begin{equation} \Delta_{min} = 2 \alpha_{1} - \phi. \end{equation}
